Abstract
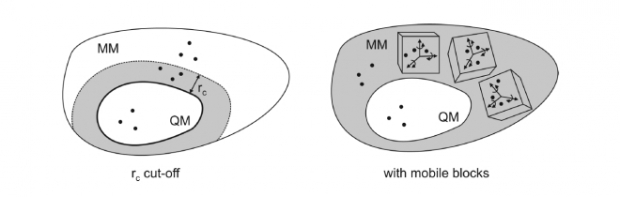
The calculation of the analytical second derivative matrix (Hessian) is the bottleneck for vibrational analysis in QM/MM systems when an electrostatic embedding scheme is employed. Even with a small number of QM atoms in the system, the presence of MM atoms increases the computational cost dramatically: the long-range Coulomb interactions require that additional coupled perturbed self-consistent field (CPSCF) equations need to be solved for each MM atom displacement. This paper presents an extension to the Mobile Block Hessian (MBH) formalism for QM/MM calculations with blocks in the MM region and its implementation in a parallel version of the Q-Chem/CHARMM interface. MBH reduces both the CPU time and the memory requirements compared to the standard full Hessian QM/MM analysis, without the need to use a cutoff distance for the electrostatic interactions. Special attention is given to the treatment of link atoms which are usually present when the QM/MM border cuts through a covalent bond. Computational efficiency improvements are highlighted using a reduced chorismate mutase enzyme system, consisting of 24 QM atoms and 306 MM atoms, as a test example. In addition, the drug bortezomib, used for cancer treatment of myeloma, has been studied as a test case with multiple MBH block choices and both a QM and QM/MM description. The accuracy of the calculated Hessians is quantified by imposing Eckart constraints, which allows for the assessment of numerical errors in second derivative procedures. The results show that MBH within the QM/MM description not only is a computationally attractive method but also produces accurate results.
