Ranking molecular crystal structures with many-body expansion QM/MM scheme
Ranking molecular crystal structures with many-body expansion QM/MM scheme
Promotor(en): T. Verstraelen /17MODEV09 / Model and software developmentMolecular crystals consist of a periodic stacking of molecules, bound by weak non-covalent forces: van der Waals, hydrogen bonds, etc. Still, these weak forces are strong enough, such that many molecular crystals are solid at room temperature. (Organic) molecular crystals are used in many industries, mostly in pharmacy, and also have promising applications in emerging technologies (e.g. organic semiconductors). One of the main engineering difficulties is the existence of so-called polymorphs. [1] Polymorphs are different metastable crystal structures for the same molecule. For example, two polymorphs of aspirin (form I and II) are depicted in Fig. 1.
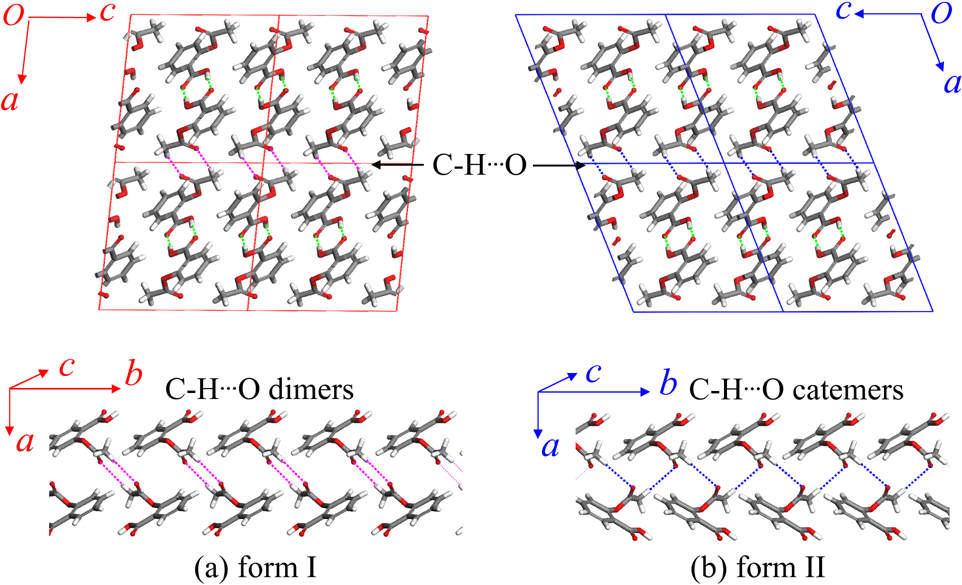
Fig. 1. Forms I and II of aspirinFrom a pharmacokinetic viewpoint, the existence of different polymorphs can be problematic. Pharmaceuticals are often produced as a crystalline powder pressed into tablets. The bioavailability of the drug (the fraction that effectively enters the bloodstream) depends on the solubility of the crystal structure, which implies that the most stable polymorphs for a given drug must be known before it can be brought to market. For example, during production one may synthesize a metastable form, which may degrade into a more stable but less active form, before it is administered.
Over the past decade, computational crystal structure prediction (CSP) has become a well-established research discipline, in which a variety of molecular simulation techniques is used to find all (meta)stable polymorphs of a given molecular crystal. [2] The stability is goverened by two main contributions to the free energy: the noncovalent interaction between the molecules and the strain energy of each molecule due to internal deformations.Goal
In this thesis, a multiscale QM/MM method will be constructed to compute the crystal structure free energy. For two atoms at long distances, only Coulomb and dispersion interactions are present, for which accurate additive models are available, such as in the MEDFF force field, which was recently developed at the Center for Molecular Modeling. [3] Short-range interactions exhibit non-additive energy contributions, which are much harder to reproduce with empirical potentials. These can be approximated with coupled-cluster (CC) calculations of molecular monomers, dimers and trimers. The number of unique monomer, dimer and trimer geometries, within a cutoff distance, is limited due to the symmetries of the crystal structure. Performing all relevant CC calculations is therefore still feasible. These CC energies will be employed to compute a truncated many-body expansion of the crystal energy. The same many-body expansion can be applied to all derivatives of the energy too, such as the Hessian or the electron density. The proposed QM/MM approach will be validated with Density Functional Theory (DFT) calculations, which can also be performed easily for the periodic case.
The QM/MM many-body expansion will be applied to (hypothetical) crystal structures submitted to previous CSP blind tests. [2] In a CSP blind test, the lewis structure of a set of drug-like molecules is published, whose crystal structures are known but kept secret. Research groups around the world are then invited to make predictions of their crystal structures, with typically about 20 groups participating. After the deadline of the blind test, all submissions are compared and an assessment is made of all methodologies used by the participants. All structures submitted in previous tests are publicly available, together with the most stable forms found in experiment.Mobility: This research topic will be conducted in the framework of a strong international network and if possible the student will be actively involved in work discussions with collaborative partners.
Motivation Appl. Phys.: The physics aspect of this thesis is the development of a multiscale method to compute the (relative) stability of molecular crystals. The engineering aspect is the implementation of the algorithms on an HPC infrastructure.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) MODELLING, MATERIALS, NANOKeywordsQM/MM, intermolecular many-body interactions, molecular crystals, structure predictionReferences
[1] Beran, G. J. O. Modeling Polymorphic Molecular Crystals with Electronic Structure Theory. Chem. Rev. 116, 5567–5613 (2016). http://dx.doi.org/10.1021/acs.chemrev.5b00648
[2] Reilly, A. M. CSP Blind Tests. (2016). https://www.ccdc.cam.ac.uk/Community/initiatives/cspblindtests
[3] 1. S. Vandenbrande et al. J. Chem. Theory Comput. 13, 161–179 (2017). http://dx.doi.org/10.1021/acs.jctc.6b00969

