The development of explicit-electron force fields in the frame of the Modern Theory of Polarization
The development of explicit-electron force fields in the frame of the Modern Theory of Polarization
Promotor(en): T. Verstraelen /17MODEV17 / Model and software developmentMany properties of molecules and materials can be computed and understood by directly solving the quantum-mechanical many-body problem of the electrons, which move in the coulomb field generated by the nuclei, and possibly feel an additional external field. (For example, the external field could be due to infrared light used to probe molecular vibrations in a spectroscopic experiment.) An exact solution from "first principles" has an exponential-scaling computational cost and is only feasible for systems counting up to 40 electrons. However, in many disciplines that employ molecular simulations, one rather is interested in macromolecular systems counting about 105 or more electrons, e.g. when simulating an entire protein or a cell membrane (See Fig. 1). In such scenarios, one typically uses so-called force field (or molecular mechanics) models, in which electrons are not explicitly described. Only the effective interactions between atoms are computed, with very approximate interaction potentials.
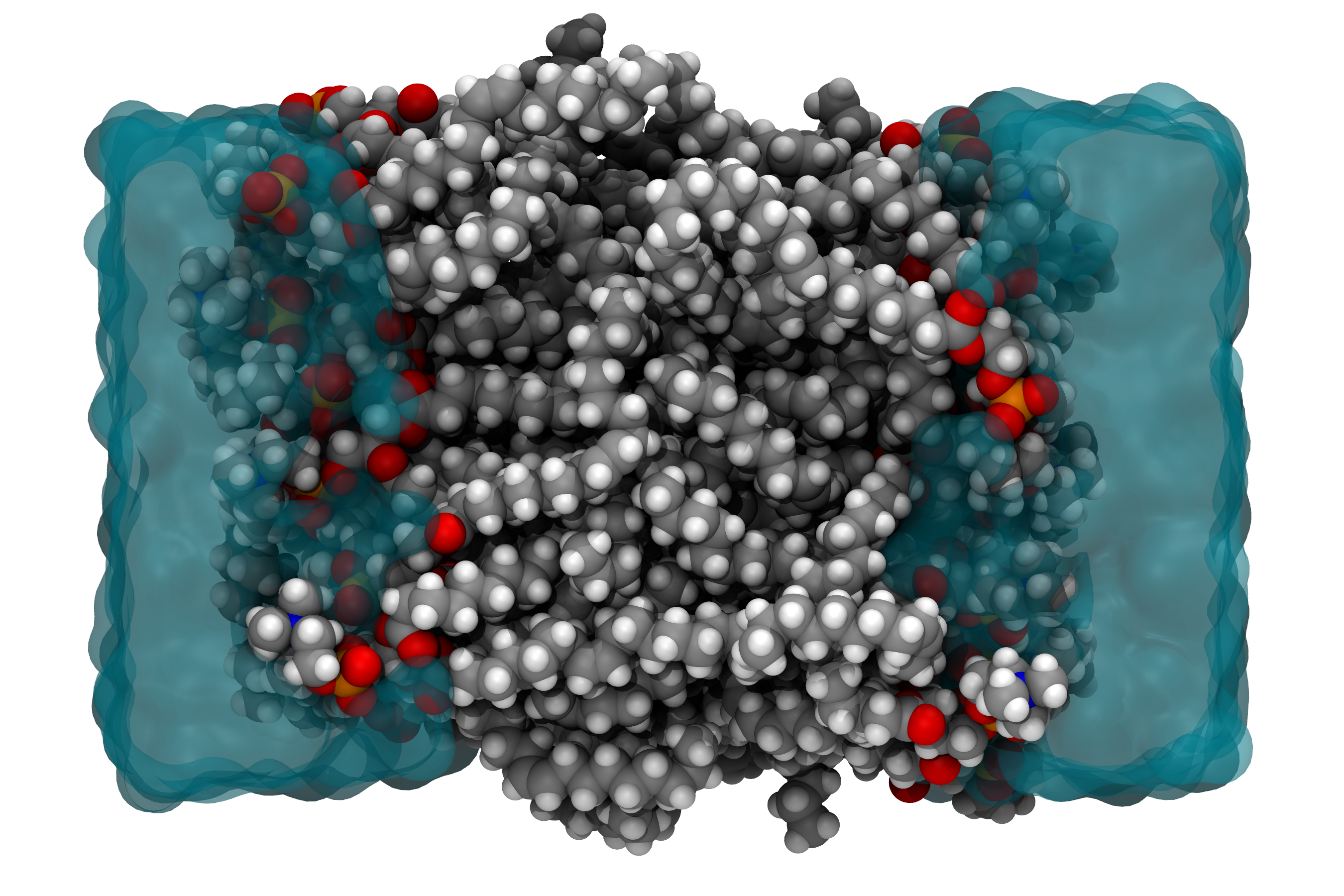
Fig 1. Molecular model of a cell membrane (cross section), which is a representative example from the field of biomolecular simulation.A fundamental limitation of force fields is the absence of a clear relation to a quantum-mechanical electronic theory. Instead, approximate interaction potentials in a force field are proposed ad hoc, using chemical intuition and educated guesses. The highly empirical nature of force fields makes it very difficult to improve their accuracy by bringing them conceptually closer to an electronic structure theory.
Goal
In conventional force fields, the only explicit particles are "atoms". Each atom represents a nucleus and a fractional number of electrons bound to it. Only the position of the nucleus is treated classically and the fractional number of electrons is described explicitly. All other electronic structure information (a lot!) is discarded and replaced by approximate interaction potentials. In this thesis, so-called explicit electron or semiclassical electron force fields will be investigated: the average positions of electrons are treated as explicit degrees of freedom. [1,2] So far, the average electron positions were never compared directly to ab initio data, which will be the main novelty in this thesis. In the modern theory of polarization, so-called Wannier (or Boys) centers can be treated as if they are centers of individual electron (pair) clouds. [3] For example, the dipole moment of a molecule can be computed from the positions of the nuclei and the Wannier centers.
More specifically, the goal of this thesis is to develop an explicit electron force field for molecules consisting of oxygen and hydrogen: H2, O2, H2O, H2O2, O3, and their protonated and deprotonated forms. These molecules form a small set for which high-level ab initio reference calculations are feasible. All long-range interactions are simple classical Coulomb interactions between point charges. At shorter distances, electrons are treated as wave packets, with a finite extent. The total electronic wavefunction is written as a simple product (!) of all these wave packets. This is obviously a drastic approximation, which is compensated for by introducing effective potentials (besides Coulomb) between the wave packets. The exact form of these effective potentials is unclear at present and different forms have been proposed.
This thesis will start from the hydrogen-oxygen model proposed by Herzfeld and validate first to what extent the positions of explicit electrons in this model correspond to Wannier centers derived from Density Functional Theory calculations. When is the correspondence satisfactory? Is the response of these positions to uniform external fields well described? How can available models be improved? One possible route is to let explicit electron parameters depend on the chemical environment instead of using universal parameters. For example, one may use different parameters for the electron pair in an H-H bond than in an O-H bond. In this part of the thesis, the student will have a lot of freedom to propose and test various ideas.Mobility: This research topic will be conducted in the framework of a strong international network and if possible the student will be actively involved in work discussions with collaborative partners.
Motivation Appl. Phys.: The physics aspect of this thesis is the development of a classical approximation of a quantum-mechanical description of the electronic structure of matter. The engineering aspect is the implementation of the model in advanced simulation software for HPCs that can handle a massive number of particles.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) NANO, MODELLINGKeywordsComputational physics, electronic structure theory, polarizable force fieldsReferences
[1] J. T. Su & W. A. Goddard. Phys. Rev. Lett. 99, 185003 (2007). http://link.aps.org/doi/10.1103/PhysRevLett.99.185003
[2] J. Herzfeld & S. Ekesan. Phys. Chem. Chem. Phys. 2, 30748–30753 (2016). http://xlink.rsc.org/?DOI=C6CP06100A
[3] R. Resta & D. Vanderbilt. in Physics of Ferroelectrics 105, 31–68 (Springer Berlin Heidelberg, 2007). http://link.springer.com/10.1007/978-3-540-34591-6_2

