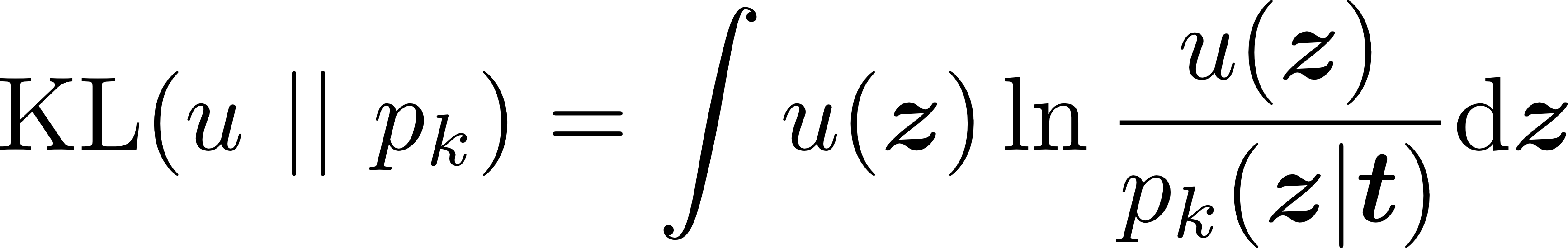Thanks to recent advances in computational techniques and the growing access to high-performance computing facilities, computationally-aided design of materials has entered a promising era with seemingly unlimited possibilities. The Center for Molecular Modeling (CMM), which is at the forefront of these advances, especially focuses on nanoporous materials such as metal-organic frameworks (MOFs). MOFs, composed of inorganic metal-oxide clusters interconnected by organic ligands, are omnipresent in a large range of applications, from energy storage and conversion, over sustainable chemistry, to biomedical applications. Moreover, the hybrid nature of MOFs makes them ideally suited to systematically engineer their building blocks, for instance by exchanging metals of the inorganic clusters, adding chemical functionalities to the organic ligands, or intentionally creating missing ligands in these materials. While synthesizing this huge variety of possible materials is a very time-consuming endeavor, the problem can be tackled efficiently by computationally predicting the best performing combinations of building blocks in a reliable and accurate way, guiding experimentalists towards a smaller set of materials to be synthesized.

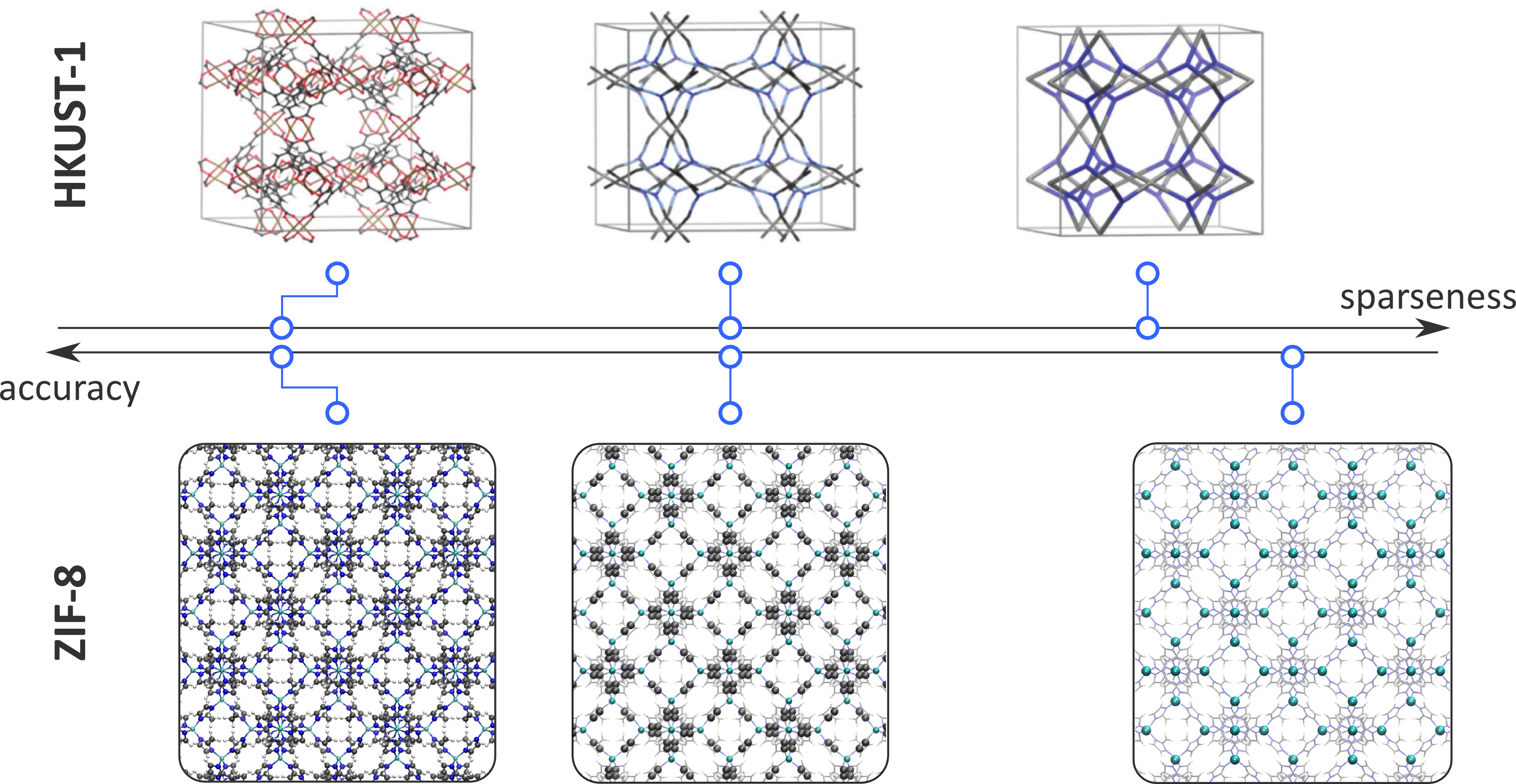
To predict the best performing combinations of building blocks, thermodynamic quantities of the MOFs are determined from simulations on the molecular scale. The most important feature of such simulations is the description of the potential energy surface. In essence, we need to deal with quantum mechanics to determine the potential energy for each molecular configuration. In order to study larger systems and longer time scales, the quantum mechanical energy surface can be approximated with force fields. When using force fields, the internuclear interactions are modelled using predefined, analytical functions which can be evaluated much faster, such that materials on the order of a thousand of atoms can be simulated for several nanoseconds. However, to comprehensively study the large-scale effects that influence the aforementioned systematic engineering of materials and reliably answer questions such as “Why do missing ligands preferentially cluster into domains of several nanometers?” and “Given two types of functionalized linkers, how will they preferentially be distributed throughout the material?”, even larger systems are necessary. To this end, reliable techniques to reduce the number of force field terms, so-called coarse-graining techniques, need to be developed and benchmarked. As indicated in Figure 1 for two prototypical MOFs, HKUST-1 and ZIF-8, coarse-graining techniques need to find a balance between accuracy and sparseness of the representation. An approach based on the variational minimization of the ‘difference’ between the free energies of the original and the sparse representation was recently introduced by two groups, leading to the ‘best’ representation given a threshold on the number of force field terms [1, 2]. This technique fits into a more universal problem akin to machine learning and data science, namely how to obtain a sparse representation of a data set, while retaining as much information as possible [3].

Goal

The variational method in this master thesis is based on two pillars. In a first step, given a coarse-grained force field consisting of k terms, we will find those force field parameters t = t1,t2,…,tk (equilibrium lengths, equilibrium angles, force constants…) that best describe the free energy of the system on a reduced, d-dimensional phase space z in a maximum-likelihood sense. This step corresponds to minimizing the Kullback-Leibler divergence between the target distribution u and the conditional contribution pk(z|t):

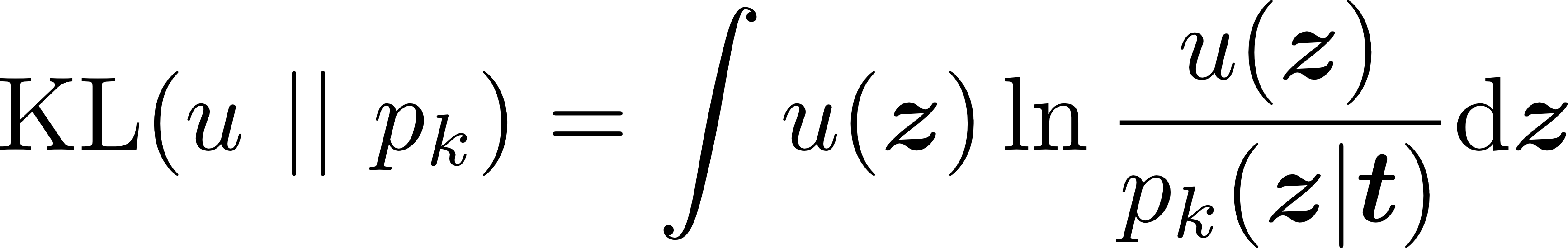
This minimization, for which elements from statistical learning techniques will be applied, requires a Monte Carlo (MC) procedure to efficiently estimate the gradient along which will be minimized [1]. While a basic MC scheme may already yield a good estimate, the student may opt to improve this estimate using for instance sequential Monte Carlo techniques or efficient stochastic optimizers, and a direct link with machine learning techniques is present. In the second step of the procedure, we will determine from a pool of force field terms the (k+1)th term that leads to a maximal increase in information. While this step can be carried out using standard optimization techniques, the performance of the resulting coarse-grained potential heavily depends on the pool of force field terms available to choose from. While one can limit itself to two-body Lennard-Jones type models, also more elaborate force field terms and the aggregation of atoms into coarse-grained beads are possible and may improve the model substantially. Here again, the student may opt to focus at this subtask if interested.

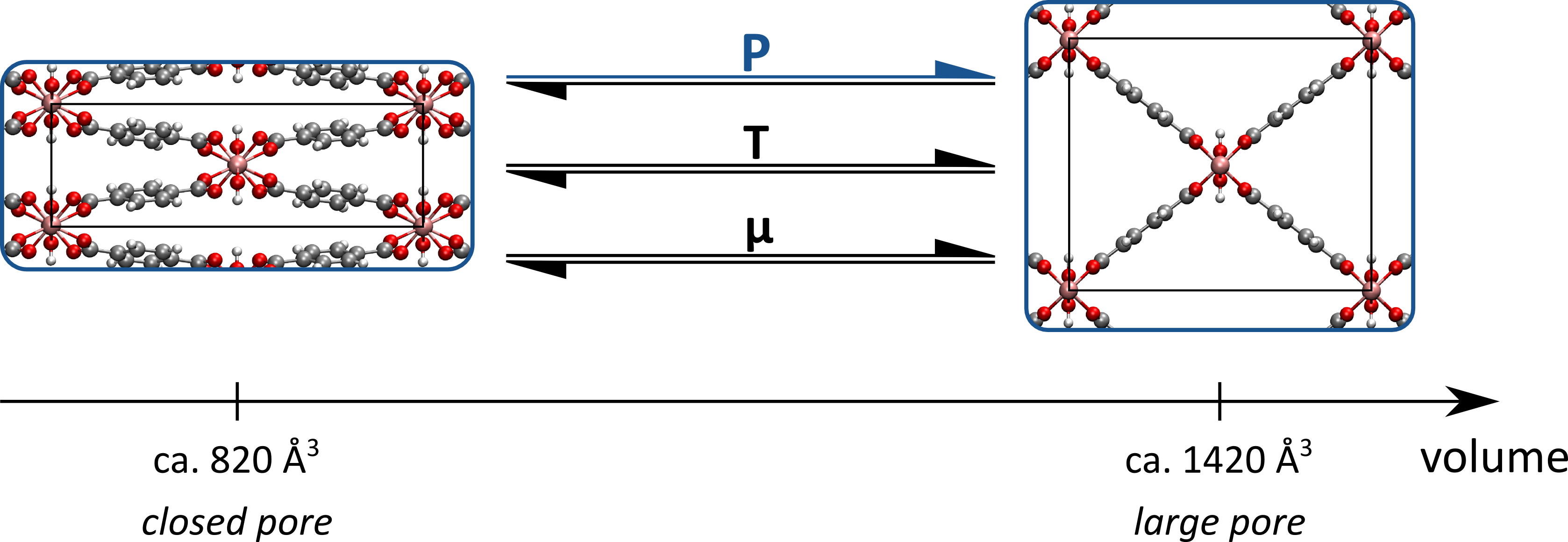
To test the several implementations in this thesis proposal, two case studies will be selected. In a first case study, 2D model systems with an analytical solution will be employed, such as the one described in Ref. [1]. In a second case study, we will use the MIL-53(Al) framework as a real-life example to quantify the trade-off between accuracy and sparseness, given our extensive experience with this material. This MOF consists of aluminum-hydroxide chains connected through organic linkers, and may experience structural transformations under the influence of external stimuli, as illustrated in Figure 3. The temperatures and pressures at which these irreversible transformations between a closed-pore and a narrow-pore phase are induced, together with radial distribution functions, are ideally suited features to test the accuracy of the different coarse-grained models developed in this master thesis. For the MIL-53(Al) framework, two approaches can be defined. In a first approach, a set of coarse-grained beads will be predefined, as well as a minimal force field to describe the bonds and bends between these beads. The procedure outlined above will then be applied to determine which force field terms need to be added to minimize the Kullback-Leibler divergence. In a second approach, this procedure may be extended by treating the coarse-grained beads as parameters, and instead of adding extra force field terms, the procedure may opt to split a given coarse-grained bead into two separate, less coarser beads.

The student will be actively coached to make him/her acquainted with the optimization techniques early in the thesis year, and to transfer necessary programming skills needed to perform the research.

Engineering & Physics aspects

Physics: use of classical mechanical models for materials modeling
Engineering: engineering of materials for applications such as storage, separation, …