Molecular Dynamics (MD) simulations of biological macromolecules are used extensively in academia and commercial research centers to simulate small (nanometer-scale) fragments of living organisms. In such a simulation, the trajectory of each atom through time is computed with Newton's equation of motion and an approximate "force field" model to compute forces acting on the atoms. Through the laws of statistical mechanics, the in-silico observations for these small model systems can be translated back to useful macroscopic properties relevant for experimental research.
With the increasing size of molecules being simulated, also the time scales of relevant processes become longer and longer. Because MD simulations proceed with time steps of about 1 femtosecond, the simulation of a one-second process would take 1015 time steps, which is still infeasible today. The longest time scales achieved in an MD simulation is of the order of milliseconds, using the ANTON computer (located in the USA). [1] Instead of performing one long MD simulation, one may also characterize the dynamics of a macromolecule with a Markov State model (MSM). The MSM summarizes the complex dynamics of the molecule as transitions between a limited collection of discrete stable states. (See Fig. 1.) The advantage of the MSM is that it can be parameterized with many short MD runs, which can be executed in parallel. [2] When applied to entire proteins consisting of over 104 atoms, the required ensemble of MD trajectories is still computationally very expensive (requires massive computing power), see for example the simulation of G protein–coupled receptor (GPCR) activation pathways using Google's Exacycle cloud-computing platform. [3] Once the MSM is constructed, the original dynamics of macromolecules can be simulated using kinetic Monte Carlo methods, reaching timescales that are even much longer than seconds.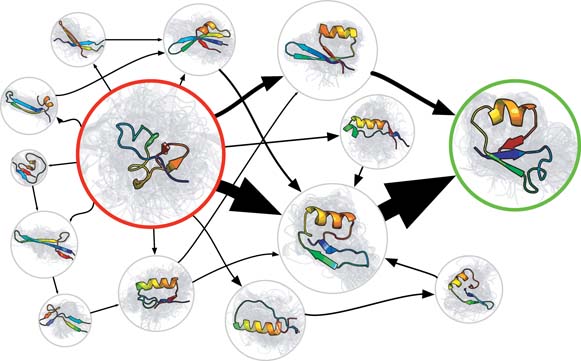

Fig 1. Visualization of a Markov State Model of a small protein. Sphere size is proportional to the stability of each state. Thickness of the arrows is proportional to the transition rates.

One of the main difficulties in the construction of a Markov State Model, is the definition of the stable states, between which transitions take place. [2] At the Center for Molecular Modeling, a new clustering algorithm for molecular conformations was recently developed, which has the potential to facilitate the development of MSMs.

Goal

In this thesis, MSMs will be constructed for Spinorphin derivatives, to characterize their structure and dynamics. Spinorphin, see Fig. 2, is a endogenous opioid heptapeptide (sequence LVVYPWT). It acts as a pain killer because it is an antagonist of the P2X3 receptors, which are normally activated by ATP to initiate pain signalling. The activity of Spinorphin and some derivatives has been characterized already in experiments. [4] We hypothesize that these activities must correlate with the presence of specific structural motifs or with the flexibility of domains in Spinorphin, because these aspects affect the ability of the heptapeptide to fit in one the P2X3 receptors. The presence of structural motifs and flexible domains can be extracted from an MSM. [2]

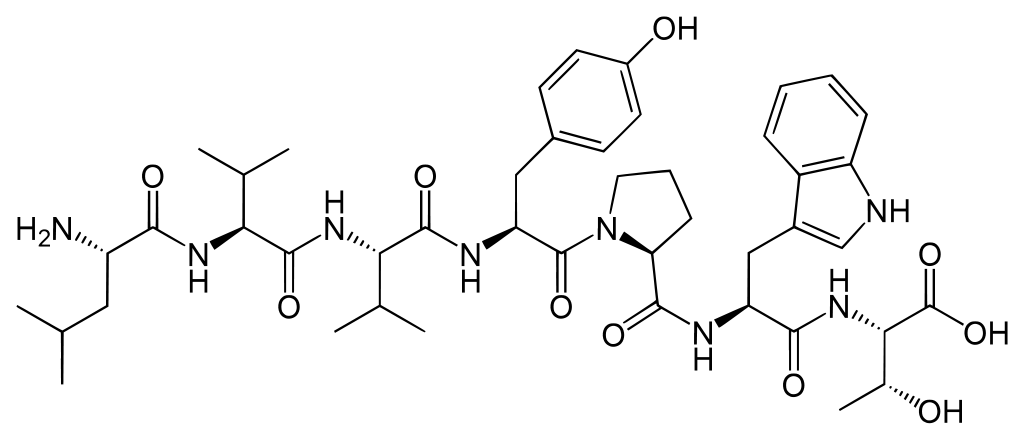
Fig 2. Spinorphin is a heptapeptide with sequence LVVYPWT.

The clustering algorithm to detect stable states is the main novelty in this thesis, which should facilitate the construction of a Markov State Model. It employs kernel principal component analysis (KPCA) [5] to reduce the large number of degrees of freedom of a peptide to a low-dimensional non-linear manifold, in which different conformational clusters are more easily separated. Simply put, the thermal fluctuations of the structure in unimportant KPCA modes are discarded. Subsequently, the trajectory in reduced dimensions is used as input for the DBSCAN algorithm [6] to detect and cluster all stable states. (DBSCAN stands for Density-Based Spatial Clustering of Applications with Noise.) Subsequently, hopping frequencies between the states are derived in order to parameterize the associated Markov State Model. The long-time-scale behavior is then modeled very efficiently by simulating hops between states in the MSM, rather than by integrating Newton’s equations for individual atoms.

The main purpose of this thesis is to work out and implement the new clustering algorithm to detect states from an ensemble of molecular dynamics simulations, as well as the methodology to derive the Markov State Model. Spinorphin derivatives, which are potentially pharmaceutically relevant, are representative test cases to validate the methodology. Moreover, other (synthetic) opioid peptides are under active development in the group of Prof. B. De Spiegeleer, where similar questions arise related to structure and activity. Details of these peptides cannot be provided here due to intellectual property restrictions.

Mobility: Mobility is not required for this thesis. The proposed topic is an ideal basis for collaborations with pharmaceutical research groups (in academia or commercial settings). An active role in such collaborations would be highly appreciated.

Motivation Appl. Phys.: The physics aspect of this thesis is the transformation of a Newtonian trajectory into a Markov State Model. The engineering aspect is the implementation of this algorithm.