Towards a reliable quantum mechanical description of excited states in open-shell transition metal complexes
Towards a reliable quantum mechanical description of excited states in open-shell transition metal complexes
Promotor(en): V. Van Speybroeck /18SPEC03 / SpectroscopyElectronic transitions are at the basis of a wide range of atomic-scale phenomena. They are intimately linked to processes involving the absorption and emission of light, which in turn impact important application domains such as spectroscopy, luminescence and photochemistry. It is therefore crucial for many materials to possess a detailed understanding of the exact electronic energy scheme, as this allows interpreting and designing complex light-based applications.
A powerful tool in this quest is computational spectroscopy. Using nothing else than a computer and some quantum mechanical equations, the position of the electronic energy levels can be predicted without any experimental input. This is often necessary, because of experimental uncertainties or a lack of insight into the experimentally observed phenomena. A particularly popular technique is that of density-functional theory (DFT). This method maps the (untractable) Schrödinger equation onto an independent-particle formalism that expresses all quantities in terms of the average electron density rather than the much more complex N-particle wave function. A crucial element in this mapping procedure is the so-called exchange-correlation functional, which expresses all deviations from a mean-field formalism into a single density-dependent term. Although this term is not exactly known, many approximate forms are available that yield accurate results.
DFT as such is restricted to ground state properties, but a time-dependent (TD) variant was proposed some years ago to also predict excited states. Linear-response TDDFT has proven successful in reproducing both excitation energies and transition probabilities. Unfortunately, it is still inaccurate when describing open-shell systems. This is mainly because of the so-called adiabatic approximation. The adiabatic approximation assumes that a time-independent exchange-correlation functional can be used, but this reduces the predicted solutions to 1 particle – 1 hole (1p1h) excitations only. Double excitations are not included, which may nevertheless play an important role in open-shell materials. A prominent example is that of spin contamination: even for three electrons in a three-level system, it can already be seen that the construction of a pure doublet or quadruplet state (spin 1/2 or 3/2) often requires taking into account double excitations as well (see figure below). A TDDFT doublet or quadruplet target state is therefore usually mixed with other spin states.
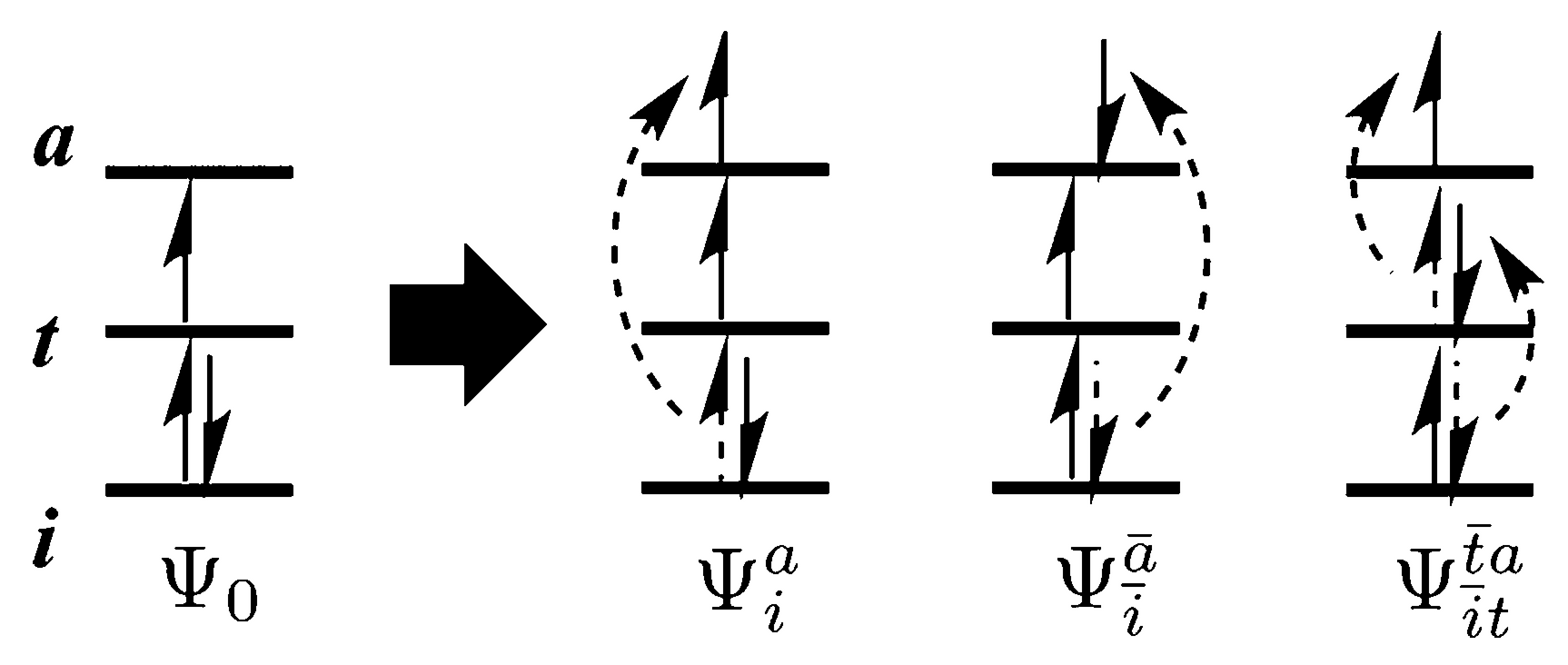
(DOI: 10.1021/acs.jpca.7b00752)Goal
For this thesis, you will investigate several approaches to obtain accurate excited-state information for open-shell systems. In particular, you will have a closer look at d-d excitations in transition metal aquo and ammine complexes (X(H2O)n(NH3)6-n2+/3+ with X a 3d transition metal, see figure below). These complexes are well known experimentally and display d-d transitions in the visual range, giving rise to a variety of colours. However, they are especially challenging to model from a theoretical point of view.
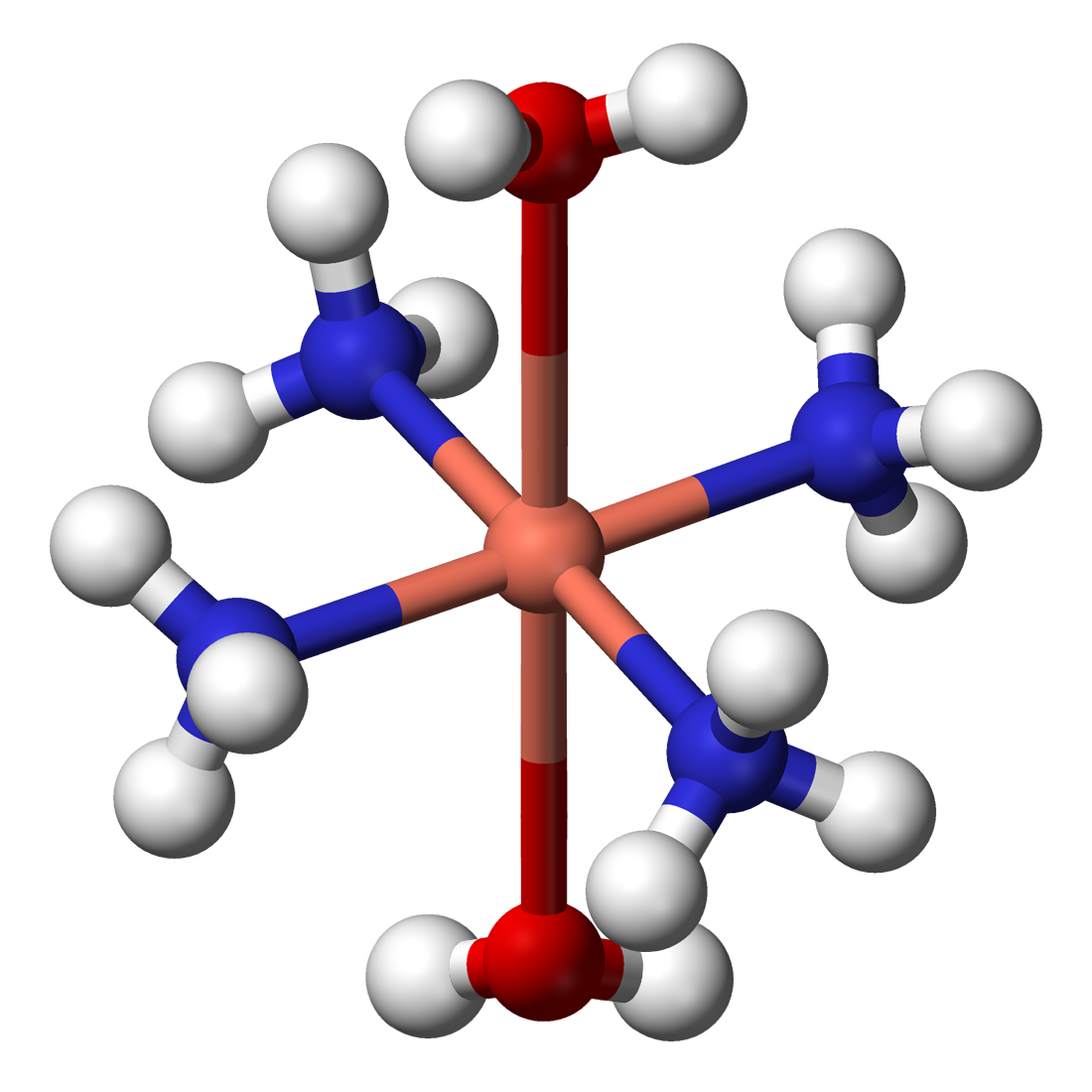
(https://en.wikipedia.org/wiki/Metal_ammine_complex)You will mainly focus on the excitation probabilities, which theory has particular difficulty getting right. Due to Fermi’s golden rule, these excitation probabilities are related to the modulus squared of the matrix element of the dipole operator |<f|r|i>|². As a result, symmetry aspects are important to take into account as well. The fully octahedral complex (point group Oh or Th), for example, will have matrix elements equal to zero due to symmetry, so mixed or symmetry-broken complexes will need to be considered.
A first part of your work will consist in a deliberate study of the traditional TDDFT formalism in combination with several possible (time-independent) exchange-correlation functionals. These data may be compared to reference data generated using high-level methods, such as CASSCF (complete active space self-consistent field) and DMRG (density matrix renormalization group). Each of these approaches is implemented in available software packages.
Secondly, you will investigate whether a good compromise between accuracy and computational load can be achieved using emerging methods, such as spin-flip TDDFT. This method remains within the adiabatic approximation, but extends the formalism to 2p2h excitations, thus promising to substantially increase the accuracy at little additional cost. Your final aim is to shed new light on the physics of open-shell excitations and identify the best quantum mechanical approach to simulate these systems.
Context for Engineering Physics students
Physics: use of quantum mechanical methods for spectroscopic modelling
Engineering: application to industrially relevant transition
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) MODELING, MATERIALS, FUNDAMENTALS, NANOKeywordsSpectroscopy, time-dependent density-functional theory, Quantum mechanics, transition metal complexesRecommended coursesSimulations and Modeling for the NanoscaleReferences
F. Vlahović et al., ‘Assessment of TD-DFT and LF-DFT for study of d-d transitions in first row transition metal hexaaqua complexes’, J. Chem. Phys. 142, 214111 (2015). https://doi.org/10.1063/1.4922111
M.E. Casida and M. Huix-Rotllant, ‘Progress in Time-Dependent Density-Functional Theory’, Annu. Rev. Phys. Chem. 63, 287-323 (2012). https://dx.doi.org/10.1146/annurev-physchem-032511-143803


