Towards realistic computational models of nanoporous materials using dimensionality reduction methods
Towards realistic computational models of nanoporous materials using dimensionality reduction methods
Promotor(en): V. Van Speybroeck /25264 / Model and software developmentBackground and problem
Metal-organic frameworks (MOFs) are composed of inorganic nodes and organic ligands, joined together with coordination bonds to form two- and three-dimensional networks. Computational models of MOFs are almost always based on an atomic-level description of the material, whereby each and every atom in the unit cell is explicitly included as a degree of freedom during the calculation of physical properties. While such an explicit atomistic treatment is naturally the most accurate approach, it does come at an excessive computational cost that imposes strong limits on the accessible time and length scales during simulations (typically in the nanosecond/nanometer regime). This is problematic because a number of interesting physical phenomena require computational models that extend far beyond this regime, into the microsecond/micrometer range. For example, flexible MOFs such as DMOF-1 or MIL-53 have the ability to transform between two structurally different phases upon changes in the external pressure or temperature. Such transitions are typically dependent on long-range correlations in the system and an accurate description of the relative stability and transition dynamics requires unit cells that are much larger than those found in conventional computational studies on MOFs [1]. Clearly, there exists a gap between the time and length scales required for an accurate description of the framework on one hand, and those accessible by computational models on the other (see Figure 1).
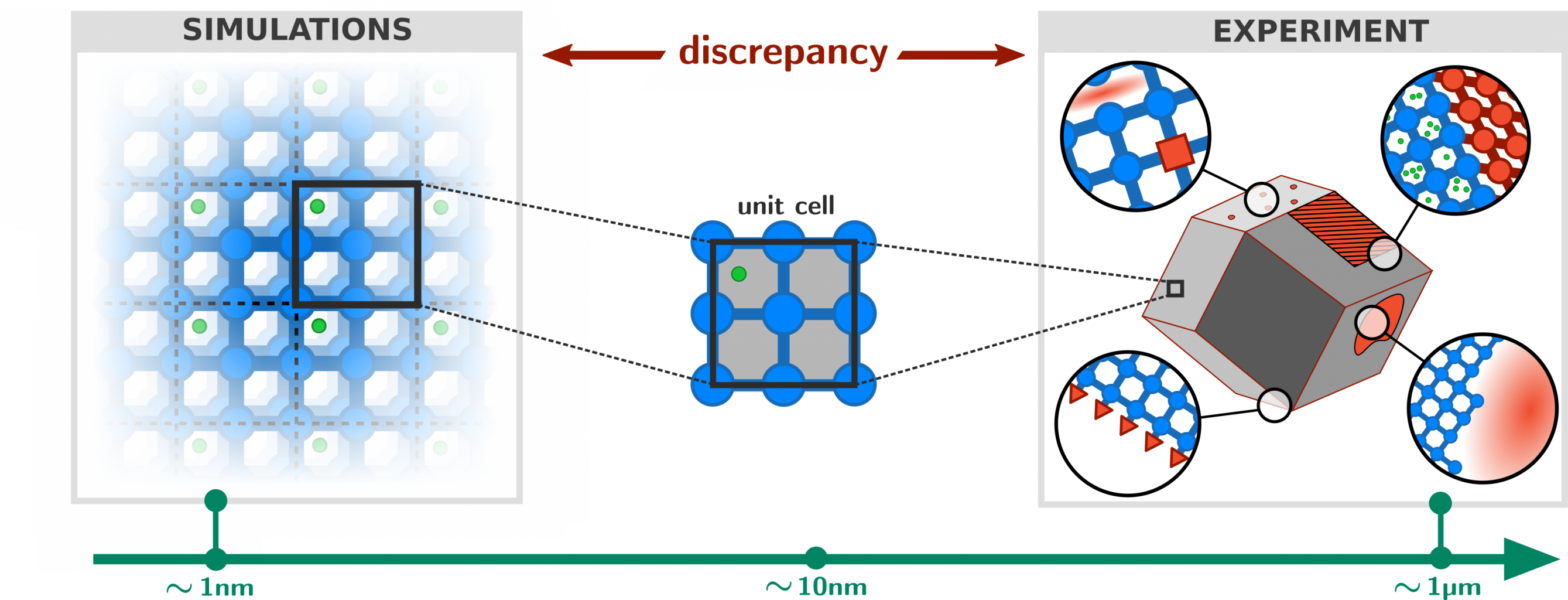
While an atomistic treatment is typically the most accurate approach in order to compute most physical properties of interest, it is often not strictly necessary to explicitly simulate each and every atom in the system. For example, global mechanical or thermal properties (bulk moduli, thermal expansion coefficients, pressure/temperature phase diagrams) often do not depend on the precise movement of each and every hydrogen in the system. This suggests that it is possible to consider so-called coarse-grained (CG) models in which irrelevant degrees of freedom are removed and only a small but important subset is retained. In physical terms, this means that several different atoms are no longer simulated separately, but are instead considered as a single group or bead (see Figure 2). The main advantage of such CG models is the fact that they are orders of magnitude less expensive to simulate, and such approaches have therefore been extensively developed and successfully applied in large biomolecular systems such as proteins. However, their development and application to MOFs is still in its infancy [2], which is partly due to the lack of a general procedure that partitions the atoms of the framework into beads such that a minimal loss of information is incurred and that the overall symmetry of the framework is preserved.
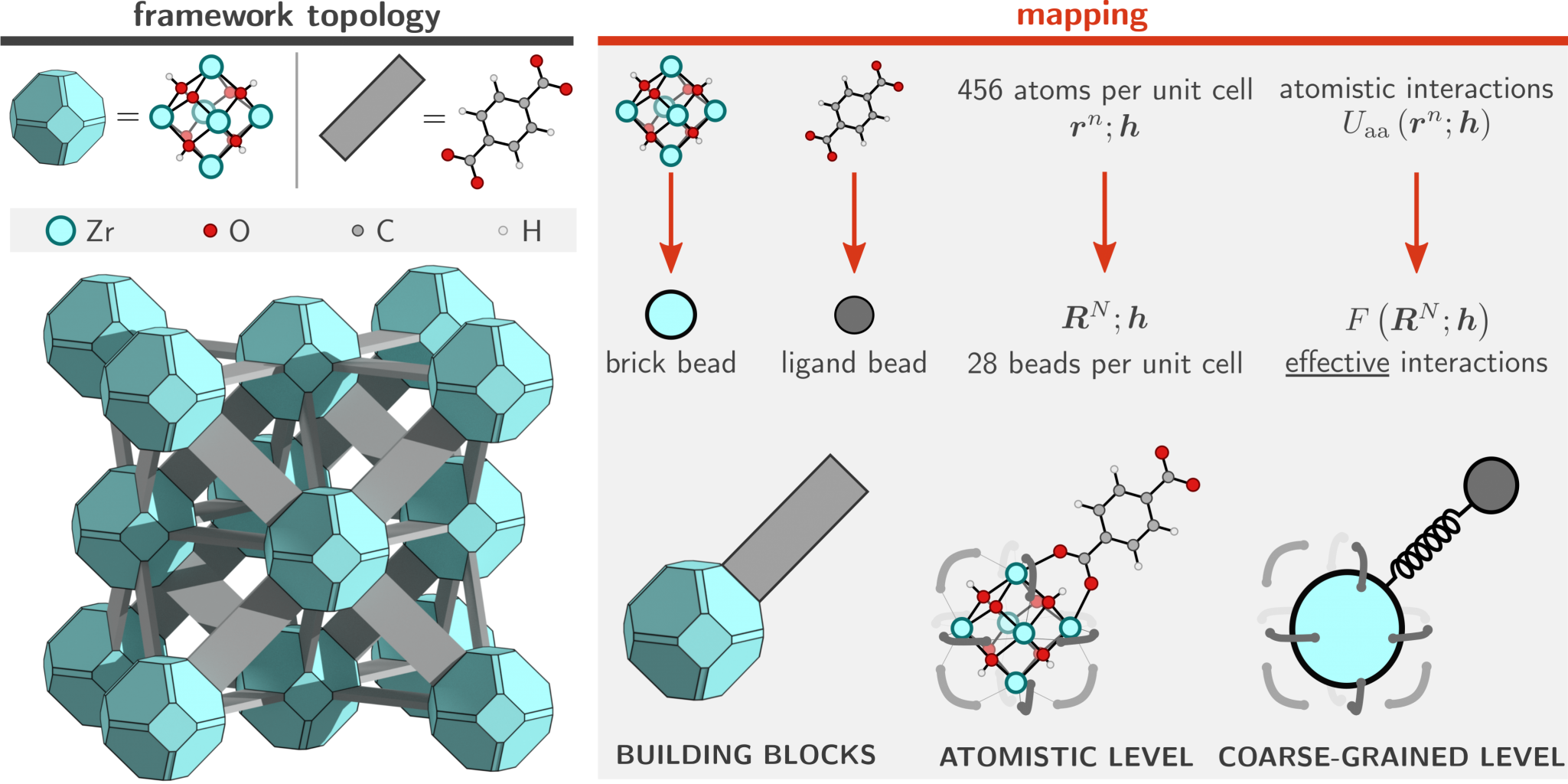
Goal
The goal of this thesis is to develop and validate an automated procedure to construct optimal coarse-grained mappings for MOFs. The ansatz is given by a recently developed metric, which quantifies the information loss associated to a given mapping based on a local characterization of the quantum mechanical interactions in the system. Optimal mappings may then be constructed by first (i) generating a set of candidate mappings which satisfy certain topology/symmetry/chemical constraints, and secondly by (ii) ranking each of those candidate mappings based on the developed metric. While a proof-of-concept implementation is available (in plain Python), further research is required to fully realize the potential of this approach. First, the method will be further developed in order to reduce the required amount of quantum mechanical input data. Second, the efficiency of the algorithm may be drastically increased by exploiting the symmetry and topology of the underlying atomistic framework as well as its chemical connectivity. While prior work is available in literature [3], it remains a significant challenge to ensure that (i) the algorithm is robust with respect to small errors in the quantum mechanical input data, and that (ii) it is universally applicable to framework materials of arbitrary size and shape. Afterwards, a series of validation experiments will be performed in which the effectiveness of the algorithm will be evaluated by investigating its results on a number of topical MOFs such as UiO-66(Zr) and MOF-5(Zn). Finally, because the computational cost of CG models is orders of magnitude lower than their underlying atomistic counterparts, the student is invited to employ the obtained models in large-scale simulations with system sizes on the order of a micrometer, and investigate size-induced changes in the physical properties of the material. Such computational studies on an experimental scale are necessary to bridge the gap between simulation and experiment, and they constitute an important component in the research goals of the CMM.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]Keywordsmolecular simulations, Nanoporous materialsReferences
[1] S. M. J. Rogge et al. Nat. Commun. 10, 4842 (2019)
[2] J. P. Dürholt et al, Dalton Trans., vol. 45, no. 10, pp. 4370-4379 (2016)
[3] M. A. Webb et al, J. Chem. Theory Comput., 15, 1199-1208 (2019)
