Metal-organic frameworks (MOFs) are crystalline porous materials, which are very promising for applications such as gas storage, drug delivery,… Since their discovery about 10 years ago, MOFs have attracted a lot of attention due to their peculiar metal-organic linker bonds. The organic linker is mostly build from a π-conjugated system (Figure 1). One could think that any metal of the periodic system could be combined with any organic linker molecule. However, not all combinations of metals and organic linkers are feasible. To understand the stability of these materials, it is of utmost importance to be able to describe the metal- π organic linker bond with the highest accuracy. It is known that precisely this metal-organic connection is the weak point of the material, leading to deformations and eventually breakage of the framework. Unfortunately electronic structure methods that are routinely used today do not always meet the requirements in terms of accuracy.

Since the 1930s, the quantum theory of molecular electronic structure is completely known. For certain classes of molecules, typically when π-conjugation or transition metals come into play, conventional electronic structure methods are computationally too expensive. The active space of interest in such molecules exceeds 16 electrons in 16 orbitals, the current size limit for an exact solution. At the Center for Molecular Modeling, a high-performance implementation of the density matrix renormalization group (DMRG) was recently developed and implemented [1]. This method allows to resolve the electronic structure exactly in active spaces of up to 40 electrons in 40 orbitals. Very recently we succeeded in providing a better electronic structure description of the oxo-Mn(salen) complex, an important industrial catalyst, which is known to be very challenging problem for electronic structure methods [2]. Figure 1 shows a few orbitals in the active space with significant partial occupation. From left to right are shown: the bonding orbital of the Mn atom with its (N,N,O,O) bridge, the interaction of an Mn d-orbital with the organic π-conjugated backbone, and a bonding orbital of Mn with the axial O atom.

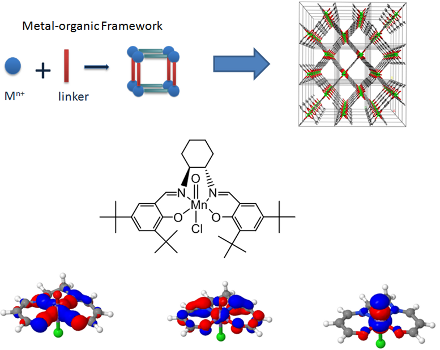
DMRG hence has the potential to accurately describe the electronic structure of the metal- π organic linker bond. In addition to a correct description of the electronic structure, it is also necessary to predict energy differences between different deformations at experimental accuracy in order to predict their stability. To bridge this gap, dynamic correlation has to be taken into account. The energy difference between the exact and the Hartree-Fock solution is called the correlation energy and can be divided into two contributions: static and dynamic correlation. Static correlation is retrieved by an accurate description of the electronic structure in the active space (with DMRG). Dynamic correlation arises due to the Coulomb repulsion between the electrons in the remaining occupied HF orbitals, which causes small partial occupations in the occupied and virtual orbitals.

Goal Fortunately, dynamic correlation can be retrieved by adding perturbation theory (PT) on top of the accurate active space solution. To be able to add PT on top of the active space solution, it is sufficient to know the N-particle reduced density matrices (N-RDM) of low rank of the active space [3][4]. These can be extracted efficiently from the DMRG solution.

Rayleigh-Schrodinger PT for active spaces relies on the generalized Fock operator. This operator has the active space solution as exact eigenstate. The difference of this operator with the exact Hamiltonian allows to set up a perturbation expansion. All expectation values required in the calculation of this perturbation expansion can be obtained from the low rank N-RDMs in the active space.

Within this master thesis, it is the intention to implement PT on top of DMRG with the intention to also include dynamic correlation. The new formalism will be tested on relevant transition metal complexes in which a metal- π organic bond is involved. The thesis builds further on two strong research lines within the Center for Molecular Modeling : (i) Fundamental many body techniques to accurately describe the electronic structure problem and (ii) Molecular level understanding of nanostructured materials. Depending on the progress made in the fundamental theoretical work, relevant applications will be taken from the active research lines of the CMM within the metal-organic framework research cell.