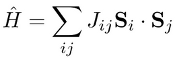Study of strongly correlated spin systems by combining density matrix embedding and geminal theory
Study of strongly correlated spin systems by combining density matrix embedding and geminal theory
Promotor(en): D. Van Neck /16_FUND05 / Many-particle physicsAlthough elegantly simple in its formulation, spin Hamiltonians capture essential aspects of strongly correlated quantum systems. A system of N interacting spins Si is described by the Hamiltonian:
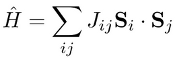
In its simplest form, a one-dimensional Heisenberg chain in which only nearest neighbour interactions are present, can be solved exactly using the Bethe-ansatz. When more complex geometries (higher dimensions, non-square lattices, see Fig. 1) and interactions are present, the exact solution via the Bethe Ansatz is missing. The physics contained in these complex models, however, is much richer than the one-dimensional counterpart, so mapping out their phase diagram is one of the major challenges in current many-body physics.
The density matrix embedding theory (DMET) [1] is a new technique that can approximately solve strongly correlated systems in the thermodynamic limit. The key observation is that the major heap of quantum correlations are centered locally around the individual spins, so the main idea of DMET is to selfconsistently embed a small local cluster, which is solved exactly, within an infinite system, which is solved on a lower level of theory. This method has been applied to a range of strongly correlated electron systems, but has not been put to the test in spin systems.
The goal of this thesis is for the student to master the ideas of DMET, and develop her/his own code in a language of choice. This involves learning a host of different concepts and techniques used in many-body quantum physics, i.e. developing a mean-field method to solve the infinite bath problem and an exact diagonalization program to solve the cluster problem.
As a first step the student would benchmark the one-dimensional Heisenberg model, which she/he can compare to a Bethe-ansatz solution. In a later stage more complex two-dimensional spin systems can be studied. Frustrated quantum spin systems will be of particular interest, considering that the exact quantum phase diagram of these systems is at present unknown and highly desirable.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) fundamentals, modelingKeywordsMany-body methods, Programming, Numerical methods, Exotic phasesRecommended coursesMany-body physics, Quantum entanglementReferences
[1] G. Knizia and G. K-L. Chan. Density Matrix Embedding Theory: A simple Alternative to Dynamical Mean-Field Theory. Physical Review Letters 109, 186404 (2012)