From Schrödinger to Newton: ab initio derived classical force fields versus machine learning potentials for zeolite properties
From Schrödinger to Newton: ab initio derived classical force fields versus machine learning potentials for zeolite properties
Promotor(en): L. Vanduyfhuys, V. Van Speybroeck /28303 / Model and software developmentBackground and problem
Ab initio molecular simulations rely, in general, on the Born-Oppenheimer approximation. Herein, the electronic Schrödinger equation is solved for a certain configuration of the nuclei, to obtain a so-called potential energy surface (PES) that represents the potential energy as a function of the nuclear coordinates. The dynamics of the nuclei is then approximated by means of classical mechanics, solving Newton’s equations of motion given the ab initio-derived forces acting on the atoms. Unfortunately, computing energy and forces for large molecular systems (> 1000 atoms) using ab initio methods and trace their dynamic evolution over large periods of time (> 1 ns) is still unfeasible even with modern supercomputers.
It is, however, possible to remarkably speed up calculations by parametrizing the ab initio PES, to create a force field (FF). In classical FFs, this parametrization is based on the many-body expansion of the potential energy V in a sum of two-body, three-body, four-body, … contributions. One of the simplest, yet most widely used, expressions for a simple FF can look like this:
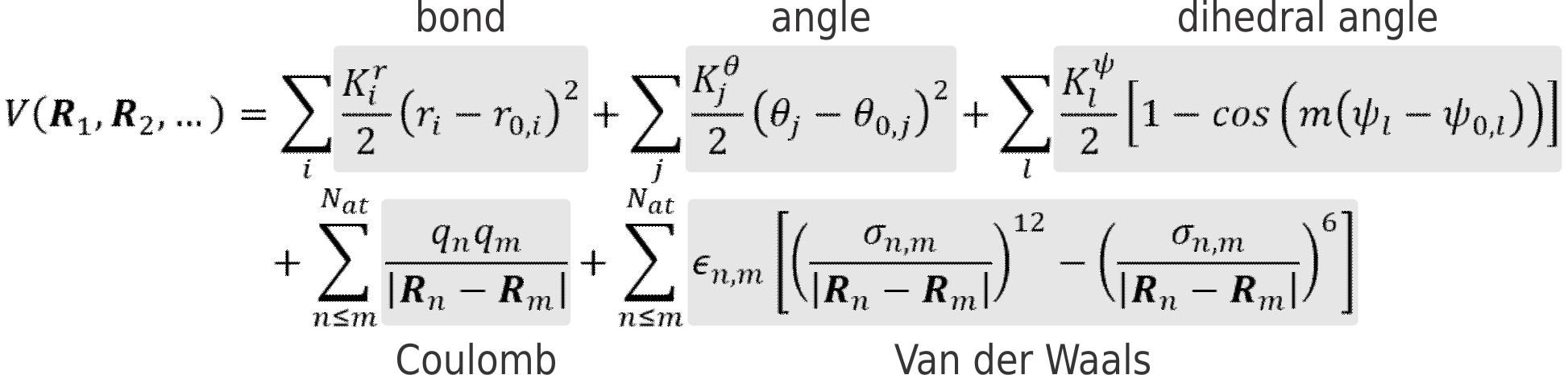
Where the first term describes the bonding potential between atoms (approximated by Hooke’s law, see Figure 1, top), the second the bending potential of an angle between three atoms and so on. Each FF term contains one or more unknown parameters that must be chosen to reproduce as well as possible the true PES of the system. As such, the development of a new force fields boils down to choosing the appropriate functional form as well as estimating the best suited values for the unknown parameters.
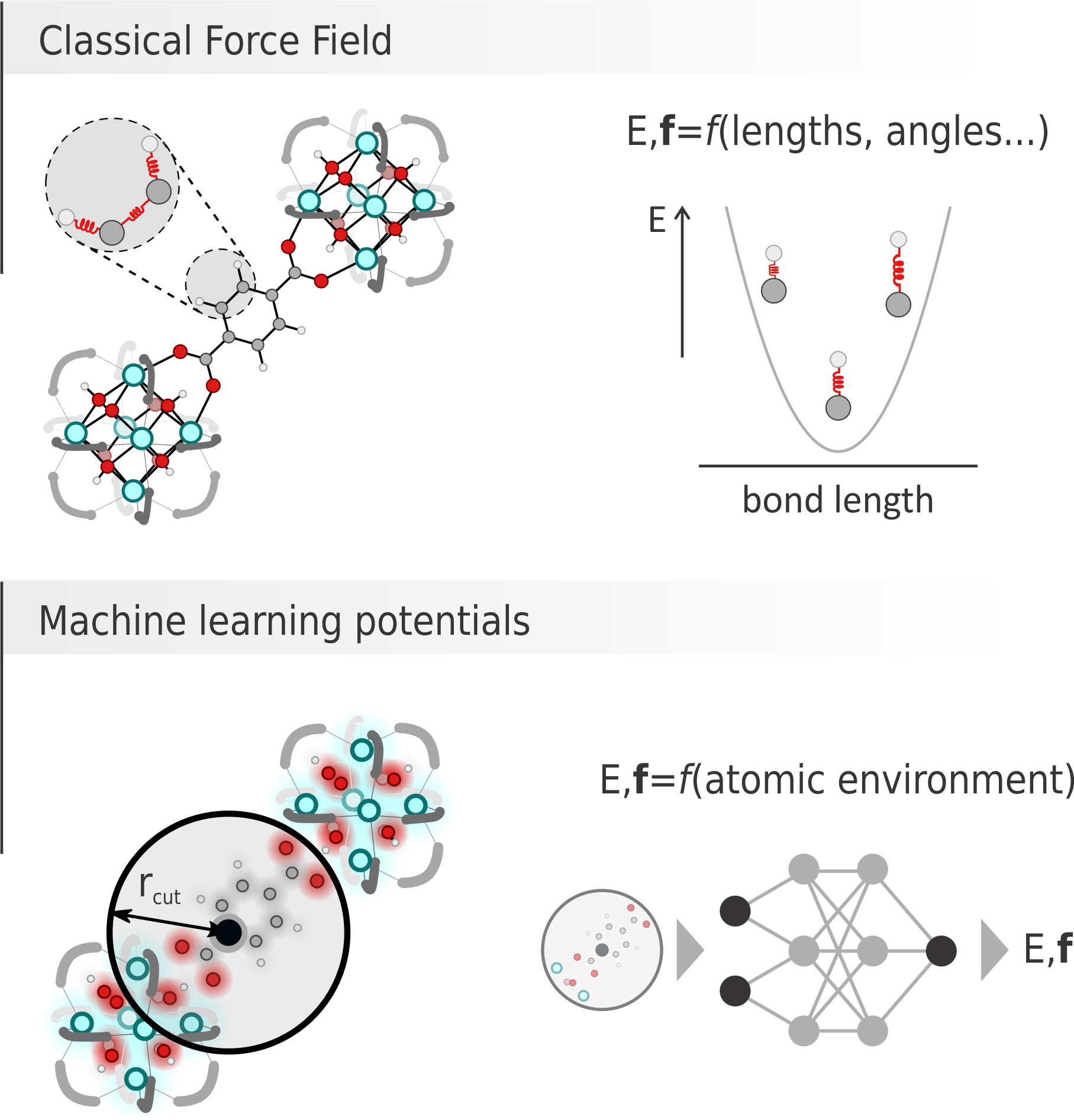
Figure 1: Graphical comparison between a classical force field, where energy and forces are computed as sum of contributions from bonds, angles… terms and a machine learning potential, where energy and forces are predicted by a neural network given the environment of each atom.
Recently, machine learning potentials (MLPs) have become primary competitors for classical FFs. There, a neural network containing thousands of parameters can be fed with an appropriate descriptor of the environment surrounding a certain atom and provide its energy and forces (Figure 1, bottom). To produce reliable results, the network needs to firstly be trained on a large set of ab initio energy and forces, with which its parameters are optimized.
On the one hand, classical FFs are very fast and easily interpretable, as each contribution to the energy directly corresponds to bonds stretching, charges interaction, etc. Unfortunately, finding the best functional form and relative parameters can be very challenging and lead to poorly accurate results. On the other hand, MLPs do not provide any obvious physical link between the results and the input structure, but the astonishingly large number of parameters in the network allows for high accuracy (sometimes at the expense of transferability). Given this set of advantages and disadvantages, this master thesis aims to derive a classical FFs and a MLP, both capable of describing a very important yet challenging class of materials, namely zeolites, and to critically evaluate their performances to unravel which methodology can provide the best results.
Goal
At the Center for Molecular Modeling, we have developed a state-of-the-art methodology to derive classical FFs [1,2,3]. Thanks to our in-house developed software packages Horton [4] and QuickFF [5], we can estimate the unknown FF parameters to reproduce reference quantum mechanical input data as well as possible. This methodology has already been extensively tested for various nanoporous crystalline materials, such as covalent organic frameworks (COFs) and metal organic frameworks (MOFs). Per contra, it has not yet been applied to investigate a very important class of inorganic materials, i.e. zeolites. Zeolites are nanoporous (i.e. have empty voids on the nanoscale) silicates (i.e. consist of SiO2 units) crystalline materials, that can exist in a plethora of different framework topologies (an example of which is depicted in Figure 2). They are widely used as adsorbent, molecular sieves and catalyst for the chemical industry. One of the known difficulties when developing classical FFs for zeolites lies in the treatment of the electrostatic interactions as well as in accurately representing the floppy Si-O-Si bend terms.
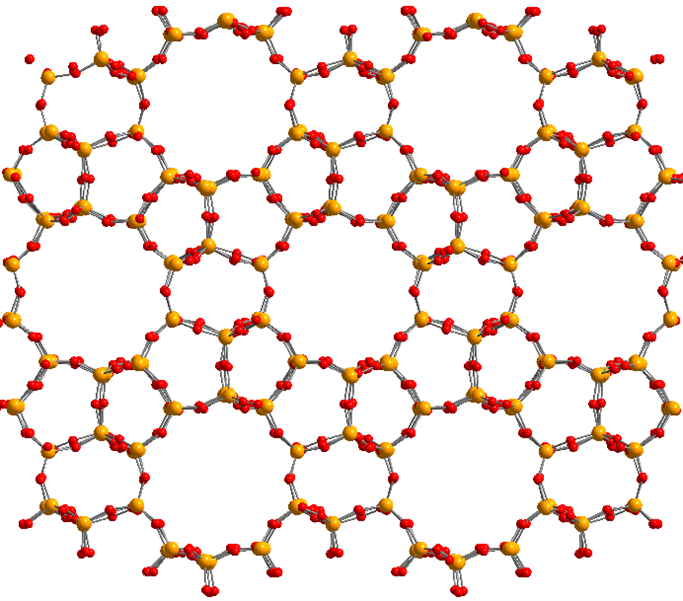
Figure 2: Illustration of the nanoporous molecular structure of the MFI zeolite framework. Yellow balls correspond to silicon, red balls to oxygen.
In this thesis, the student will derive both classical FFs and MLPs for well-characterized zeolite framework topologies, for which experimental and theoretical data are available. First, they will make themself familiar with the methodology using Horton and QuickFF for classical FFs and the NequIP package [6] for the MLPs. Second, the two approaches will be evaluated by performing various molecular simulations to compute the structural (equilibrium geometry), mechanical (bulk modulus), thermal (thermal expansion coefficient) and adsorption properties (water and methanol uptake) of the material. By comparing with experimental and/or computational data from literature, it will become possible to quantify weaknesses and strengths of both methodologies, to understand which one performs the best.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]KeywordsQuantum mechanics, Born-Oppenheimer surface, potential energy, force field, electrostatic interactions, chargesReferences
[1] L. Vanduyfhuys et al., J. Comput. Chem., 2018, 39(16), 999
[2] L. Vanduyfhuys et al., J. Comput. Chem., 2015, 36(13), 1015
[3] T. Verstraelen et al., J. Chem. Theory Comput., 2016, 12(8), 3894
[4] HORTON, https://theochem.github.io/horton/2.1.1/index.html
[5] QuickFF, http://molmod.github.io/QuickFF/
[6] arXiv:2101.03164
