Experimental investigation of new materials, medicines or other species requires spectroscopic characterization of the prepared samples to reveal their structure. Vibrational spectroscopy is a very important class of techniques including, amongst others, infrared (IR) spectroscopy, Raman spectroscopy and inelastic neutron scattering. The result of these measurements is an absorption or transmission rate of radiation, as a function of the wavenumber.

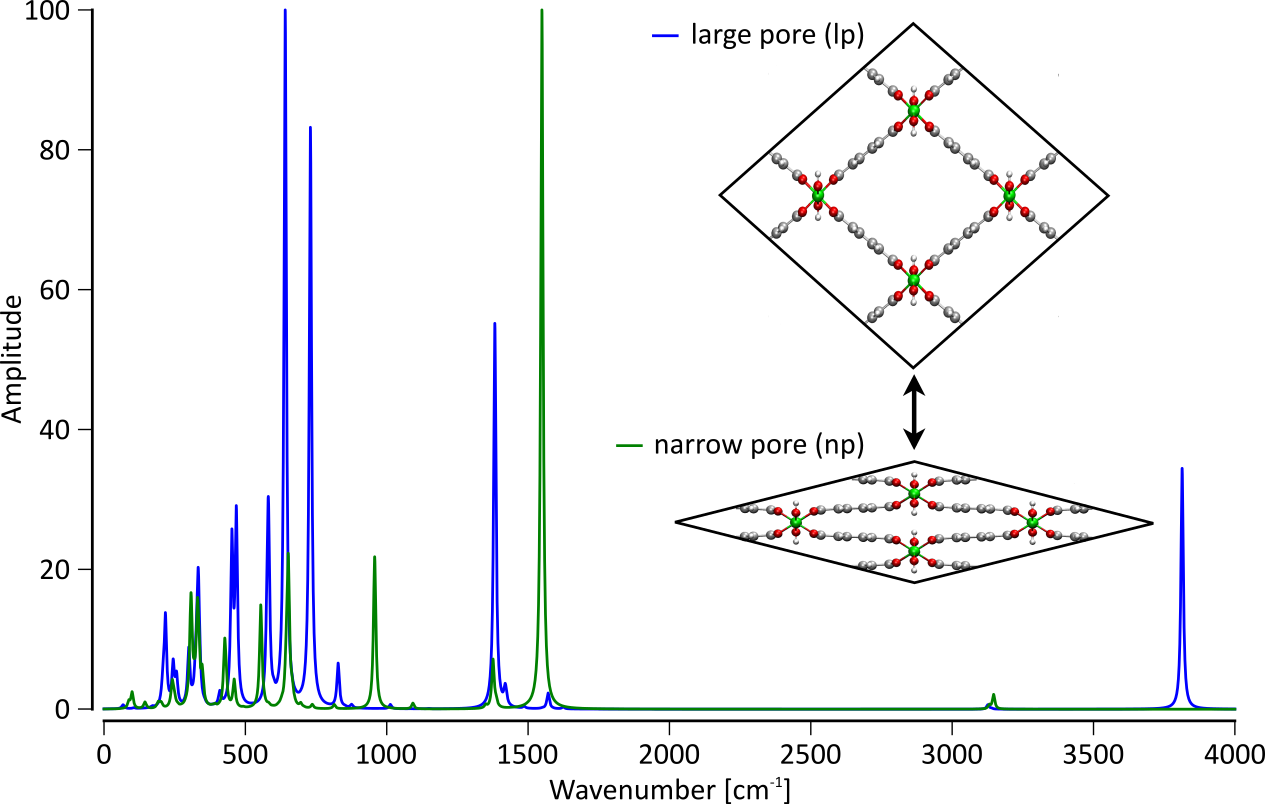
Fig. 1 shows two theoretical IR spectra of the MIL-53(Al) metal-organic framework. Theoretical IR spectra, computed at the PBE-D3 level of theory, in the large-pore form (blue, structure visualized in inset) and in the narrow-pore form (green).

These spectra can be used as a fingerprint of a sample containing one or more compounds of interest. Every peak can, in principle, be associated with a vibrational eigenmode at the atomic scale. Experimentally, the assignment of peaks to groups of atoms (e.g. CH3) is done empirically and allows one to unravel the composition of the sample. Obviously this empirical approach is only applicable to relatively simple molecular structures.

Vibrational spectra can also be predicted with molecular simulations. In the simplest case, the potential energy felt by the nuclei is approximated with a second-order Taylor series. The matrix with second order derivatives in this Taylor series is called the Hessian, which describes the atomic vibrations as a set of coupled oscillators. The eigenvectors of the mass-weighted Hessian are a basis in which the oscillators decouple, each having a single vibrational frequency that can be compared to experiment. The eigenvectors reveal which atoms are involved in each vibrational mode. Even though the eigenvectors cannot be directly compared to experiment, they do provide essential clues for the assignment of peaks in experimental spectra.

Goal

In a realistic spectrum, there are often many near-degenerate low frequencies (wavelengths below 1000 cm-1) with eigenmodes (obtained by a computer simulation) that are delocalized over the entire molecule or crystalline solid. This prohibits a straightforward interpretation of the eigenmode. One can apply an a posteriori unitary transformation to a set of near-degenerate modes such that they become more localized in space. The localized vectors have only a few significant non-zero elements for atoms that are close to each other. The spatial locality of the modes makes them easy to interpret, which is valuable for the assignment of peaks in an experimental spectrum. However, this post-hoc analysis is laborious, error prone and only applicable when clear sets of near-degenerate eigenmodes can be easily identified. The goal of this thesis is to develop and validate a more robust alternative that can be applied with a minimum of subjective choices.

A theoretical framework will be provided at the beginning of the thesis to define spatially localized modes that are almost eigenmodes of the mass-weighted Hessian matrix. The basic idea is to express a matrix diagonalization as the minimization of an objective function, i.e. the sum of the squared off-diagonal elements of the transformed Hessian. The variables in this optimization are the eigenvectors. Other criteria may be added to this objective function to impose the spatial locality of the eigenmodes.

In the thesis, the provided theory is further developed and implemented. Its effectiveness will be tested with realistic test cases, such as MIL-53(Al). Obviously, the student has the freedom to propose alternative methods and to explore extensions of the theory to analysis spectra derived from molecular dynamics simulations. This thesis will be carried out in close collaboration with prof. Van Speybroeck and prof. Ghysels

Mobility
This research topic will be conducted in the framework of a strong international network and if possible the student will be actively involved in work discussions with collaborative partners.

Motivation Appl. Phys.
The engineering aspect is the development of a practical computational tool. The physics aspect is the analysis of simulated and experimental vibrational spectra.