Layers under stress: Derivation of stress algorithms to control the interlayer shearing in 2D covalent organic frameworks
Layers under stress: Derivation of stress algorithms to control the interlayer shearing in 2D covalent organic frameworks
Promotor(en): V. Van Speybroeck /25437 / Model and software developmentBackground and problem
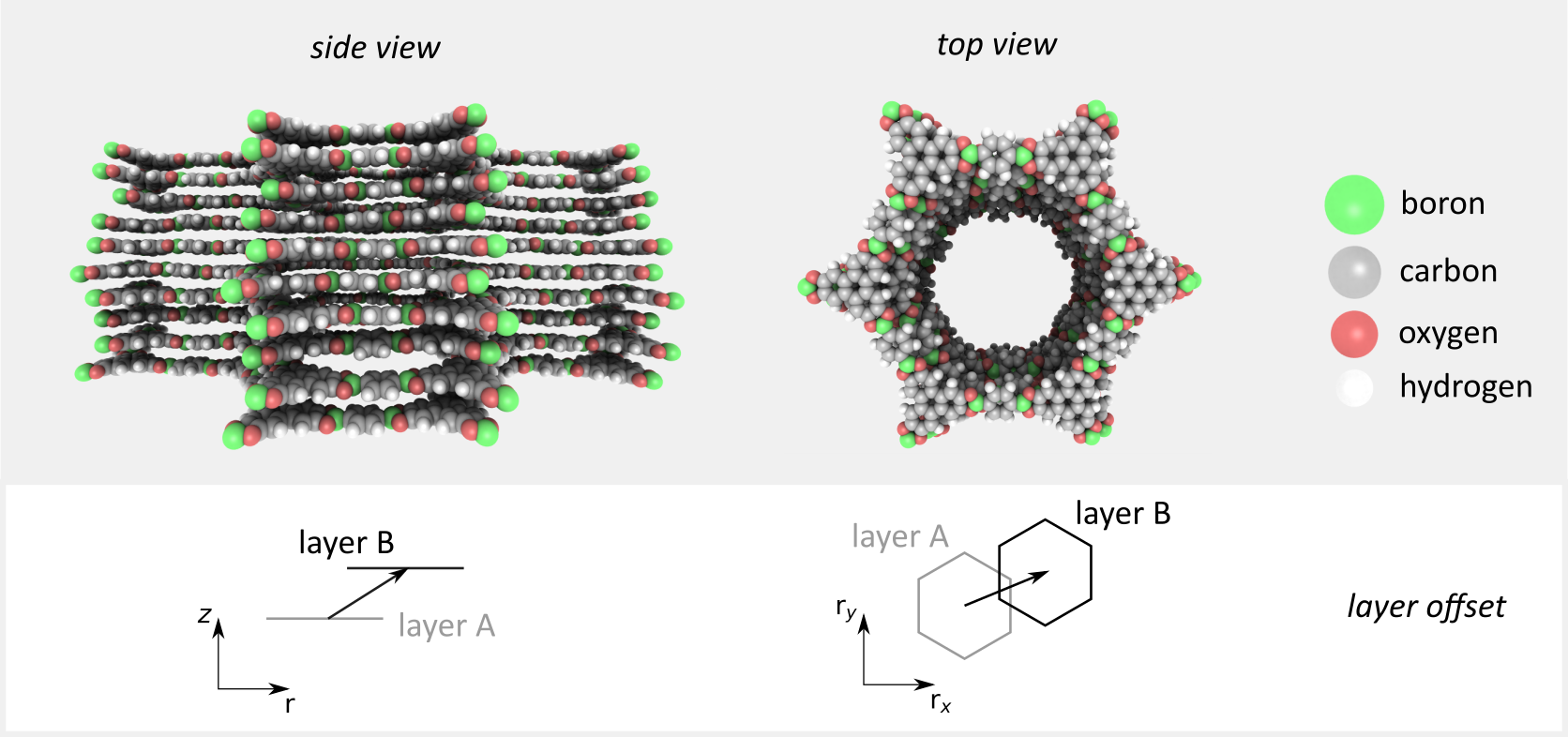
Nanoporous framework materials are highly promising for several day-to-day applications such as energy storage, gas separation, and heterogeneous catalysis given their unique combination of appreciable structural order and enormous yet tunable porosity. One such class of materials are covalent organic frameworks (COFs), consisting solely of organic moieties which makes them extremely stable despite their porosity [1]. In general, COFs can be subdivided into 3D materials, which are completely connected by strong covalent bonds, and their 2D counterparts, which form layered structures. This latter category of COFs is capable of forming 1D channels, similar to graphene (see Figure 1), thereby forming extended electron clouds that promote charge migration and make these materials exceptionally interesting for photocatalysis and use in photoactive devices. Adjacent layers of these 2D COFs interact through much weaker forces, such as dispersion and Coulomb interactions. This renders these layers highly dynamic and gives rise to different stacking orders [2], making it challenging to experimentally characterize the dynamics of these materials [3], as we demonstrated recently. As these dynamics may also jeopardize their stability against shear stresses it is therefore crucial to understand how one can tuning the components of these 2D COFs to optimize their resilience against interlayer shearing.
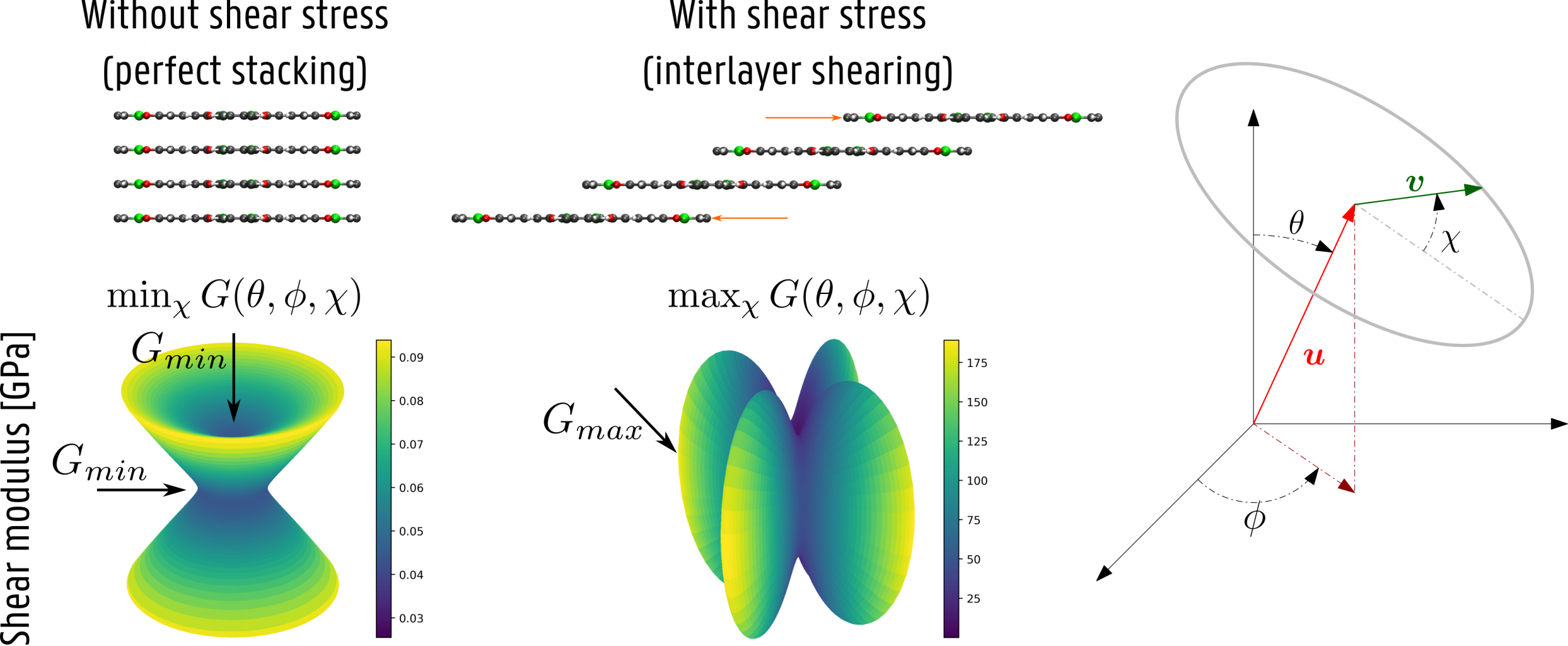
In recent years, the Center for Molecular Modeling (CMM) has developed various computational tools to study the behavior of nanoporous materials under external stimuli such as temperature and mechanical pressure, and we have proven their reliability through comparison with experiment [4]. However, these state-of-the-art methods assume a hydrostatic pressure, and cannot take into account the shear stresses that easily destabilize 2D COFs. Until now, one has to rely on determining the relevant mechanical moduli near equilibrium (see Figure 2), which provides only limited information for the material’s resilience against shear stresses which are crucial to induce interlayer shearing. The development of a reliable protocol to predict the response of 2D COFs on more general stresses would therefore enable the in silico screening of stacking in 2D COFs, paving the way for their use in several industrial applications.
Goal
The aim of this thesis is twofold. In a first step, the student will become familiar with the basics of statistical physics and ensemble theory, obtaining the necessary background on the requirements for the derivation of a constant-stress ensemble. Here, the student will benefit from the expertise present at the CMM obtained during the derivation of constant-temperature and constant-pressure ensembles [5]. With this knowledge, it is the aim to thoroughly validate the current implementations of the two constant-stress ensembles available in our in-house software code Yaff [6, 7], where necessary extending them with new constant-stress algorithms from literature. In a second step, the algorithm will be applied to study the shear stress necessary to induce layer shearing in 2D COFs and identify the weakest directions along which this shearing motion can be induced. While we will start with calculating the necessary shear stress for existing COFs, it is the aim to investigate how the effect of interlayer shearing can be counteracted by the inclusion of judiciously chosen, alternative building blocks in the material [2]. The results obtained in this thesis will be compared with results based on calculating the mechanical moduli, which are easier to determine but only provide information on the material near equilibrium.
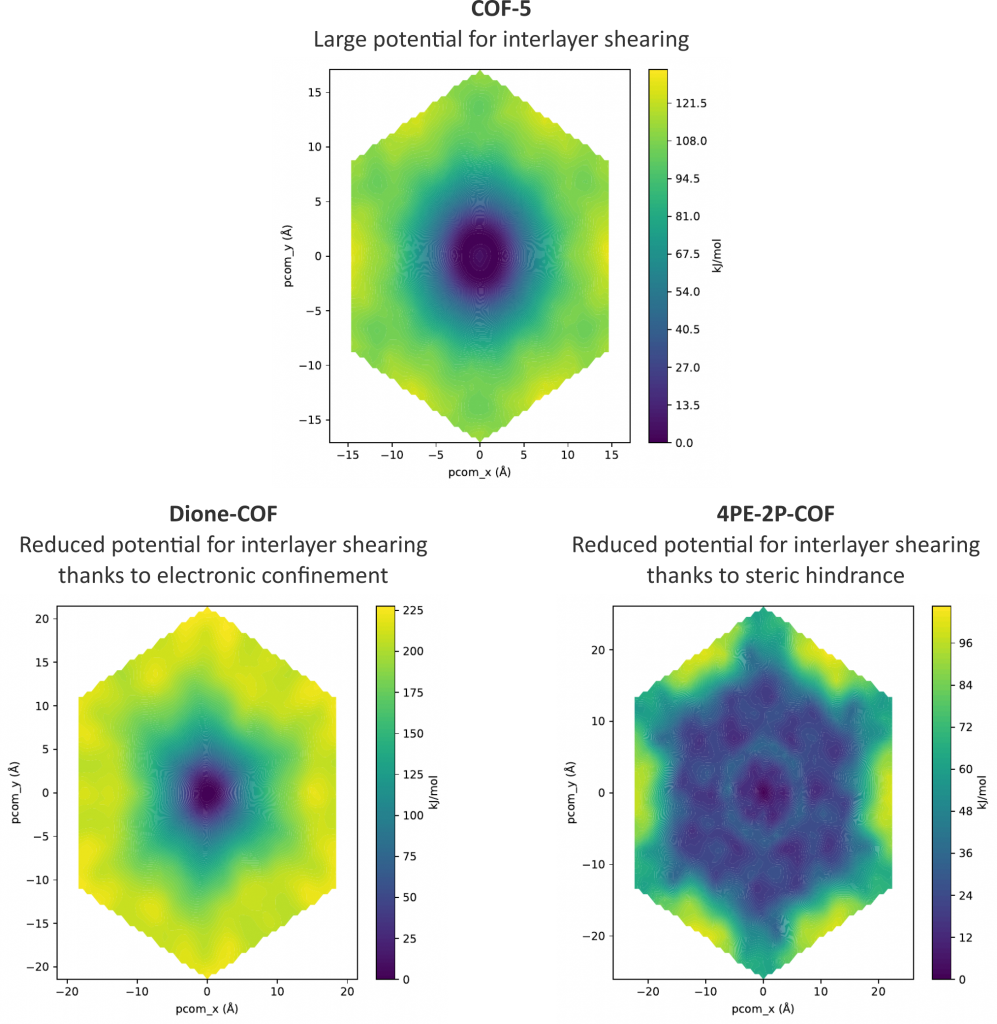
To reach the final goal of limiting the interlayer shearing in 2D COFs, different pathways can be chosen, such as the inclusion of extended linkers, linkers with bulky substituents, linkers with multiple aromatic moieties, or linkers containing atoms with large differences in electronegativity. By choosing building blocks with a particular shape or with large partial charges, resulting in a lock-and-key-like molecular conformation, one could fix the alignment of adjacent layers due to steric hindrance or electronic confinement [8]. These effects can be efficiently characterized through the free energy surface (FES) which dictates the behavior of the system. For instance, for COF-5, a conventional COF lacking an intrinsic mechanism to counteract interlayer shearing, the FES in the top pane of Figure 3 is characterized by a broadly distributed minimum. This indicates that adjacent layers have a large conformational freedom and can shear easily, thereby jeopardizing the channel size in the material. However, by introducing electronic confinement or steric hindrance in the material, as in the bottom panes of Figure 3, the spatial extent of the minimum in the FES is strongly reduced, fixing the relative position of adjacent layers. Following these pathways, newly in silico designed COFs will be optimized in this thesis to alter the dispersion and/or Coulomb interactions between the different layers, providing the necessary resistance to interlayer shearing. Subsequently, the effect of introducing guest atoms on the shearing will be probed, corresponding to the molecular environment of the layers during the use of these COFs for practical applications. The results obtained in this thesis can then be critically compared with preliminary trends that we extracted earlier based on the stacking profiles for these 2D COFs, as visualized in Figure 1.
The student will be actively coached to make him/her acquainted with the advanced simulations techniques early in the thesis year, and to transfer necessary programming skills needed to perform the research. A strong interest in programming is, however, a prerequisite.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]KeywordsImplementation, Covalent organic frameworks, Ensemble, Cauchy stress, ShearingReferences
[1] A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, “Porous, crystalline, covalent organic frameworks,” Science, vol. 310, no. 5751, pp. 1166-1170, 2005.
[2] S. B. Alahakoon, S. D. Diwakara, C. M. Thompson and R. A. Smaldone, "Supramolecular Design in 2D Covalent Organic Frameworks," Chem. Soc. Rev., vol. 49, no. 5, pp. 1344-1354, 2020.
[3] S. Borgmans, S. M. J. Rogge, J. S. De Vos, C. V. Stevens, P. Van Der Voort and V. Van Speybroeck, “Quantifying the likelihood of structural models through a dynamically enhanced powder X-ray diffraction protocol,” Angew. Chem. Int. Ed., 2021. DOI: 10.1002/anie.202017153.
[4] S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, “Reliably Modeling the Mechanical Stability of Rigid and Flexible Metal-Organic Frameworks,” Acc. Chem. Res., vol. 51, no. 1, pp. 138-148, 2018.
[5] S. M. J. Rogge, L. Vanduyfhuys, A. Ghysels, M. Waroquier, T. Verstraelen, G. Maurin and V. Van Speybroeck, “A Comparison of Barostats for the Mechanical Characterization of Metal-Organic Frameworks,” J. Chem. Theory Comput., vol. 11, no. 12, pp. 5583-5597, 2015.
[6] M. Parrinello and A. Rahman, “Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method,” J. Appl. Phys., vol. 52, no. 12, pp. 7182-7190, 1981.
[7] R. E. Miller, E. B. Tadmor, J. S. GIbson, N. Bernstein and F. Pavia, “Molecular Dynamics at Constant Cauchy Stress,” J. Chem. Phys., vol. 144, no. 18, p. 184107, 2016.
[8] L. Ascherl, T. Sick, J. T. Margraf, S. H. Lapidus, M. Calik, C. Hettstedt, K. Karaghiosoff, M. Döblinger, T. Clark, K. W. Chapman, F. Auras and T. Bein, "Molecular Docking Sites Designed for the Generation of Highly Crystalline Covalent Organic Frameworks," Nat. Chem., vol. 8, no. 4, pp. 310-316, 2016.
