Investigating electron correlation effects via advanced many-body techniques to describe the photovoltaic properties of complex perovskites
Investigating electron correlation effects via advanced many-body techniques to describe the photovoltaic properties of complex perovskites
Promotor(en): V. Van Speybroeck, F. Verstraete /28205 / Many-particle physics, Nanoporous materialsBackground and problem
The Hartree-Fock (HF) procedure is a fully quantum mechanical method that finds the wavefunction of a system by solving the Schrödinger equation in a self-consistent manner. However, while HF exactly accounts for electron exchange, it completely neglects electron correlation. Density functional theory (DFT) can mitigate this challenge, as it solves for the ground state electron density instead of the multidimensional wavefunction in HF, and as it can approximately account for electron correlation via an appropriate choice of the so-called exchange-correlation functional. DFT is therefore the method of choice in many solid-state investigations. However, while some DFT functionals achieve chemical accuracy for certain properties in simple systems such as closed-shell organic molecules [1], it fails for systems that exhibit strong electron correlation, such as metal halide perovskites (MHPs).
MHPs exhibit extraordinary properties for photovoltaic applications, such as high absorptivity, long electron-hole diffusion lengths, and high charge mobility [2]. Recently, the maximum obtained solar cell efficiency of perovskite absorbers has risen substantially, up to 25.7%. MHPs adopt the perovskite crystal structure, with an ABX3 chemical formula containing B metal cations and X halide anions. Since strongly correlated electron fluctuations (dispersive interactions) can occur between the A cations and the metal halide network, DFT typically fails to describe these materials. Moreover, MHPs doped with rare-earth compounds show improved photovoltaic properties. However, these (post-)transition metals occupying the B sites exhibit open d-and f-electron shells for which static electron correlation is important in addition to the aforementioned dynamic electron correlation, further limiting the usage of DFT.
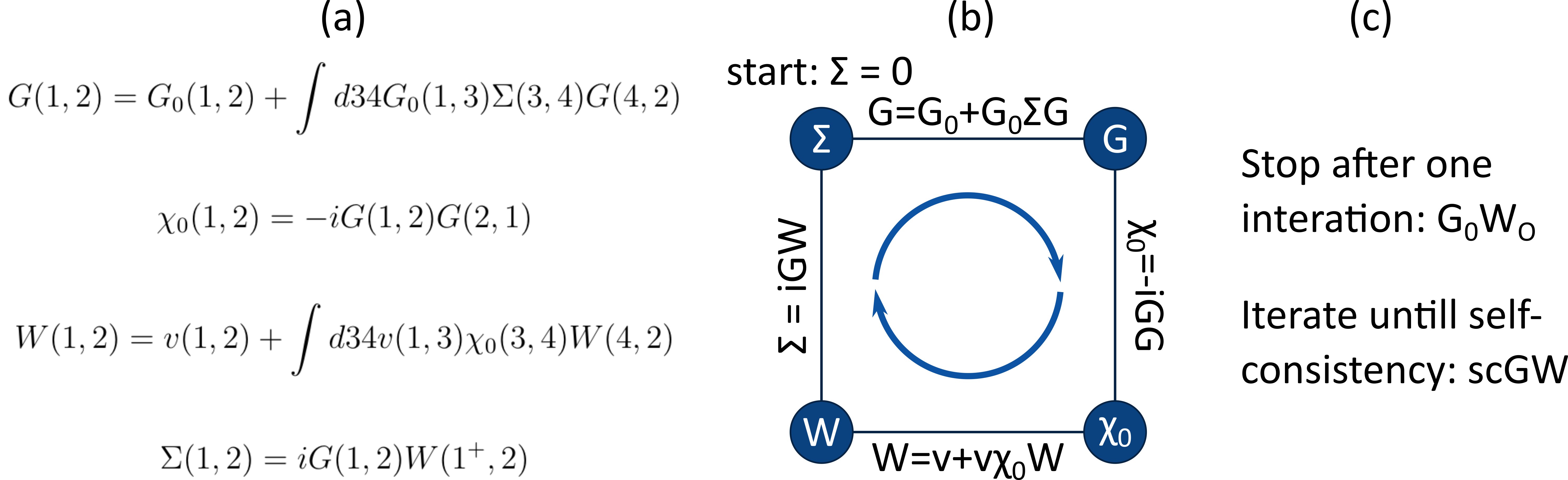
Figure 1: (a) The reduced Hedin equations after the GW approximation, (b) these equations are coupled as shown by the diagram. (c) Within the GW approximation different approaches are possible to determine the self-energy, such as the scGW and G0W0 methods.
To accurately describe these technologically relevant yet complex MHP materials, fundamental many-body methods such as the Green’s function many-body perturbation approach (GW) are necessary. From many-body perturbation theory, the coupled Hedin’s equations can be derived [3]. The GW approximation simplifies these coupled equations to those shown in Figure 2. The GW method is used to derive the self-energy (Σ), which incorporates the interaction of a quasi-particle and the interacting system by taking into account screened Coulomb interactions (W). The electron quasiparticle combines the electron itself as well as its effect on the system with which it interacts, which is necessary since adding or removing electrons to the system also alters the positions of the other electrons in the systems. As shown in Figure 1, different approaches are possible to derive the self-energy. For instance, it can be derived self-consistently (the scGW method) or with only one iteration such that the self-energy is determined by the initial Green’s function G0 (the G0W0 method). With the self-energy obtained in the GW method, an effective potential can be constructed to find quasi-particle energies even for strongly correlated systems such as MHPs.
Goal
During the thesis, you will dive into many-body theory to familiarize yourself with the complex concepts underlying the GW method and afterwards apply both the GW method and DFT to determine the ground state energies and band structure of different perovskite systems. The aim of this thesis is twofold. First, we want to investigate to which extent DFT and GW, with their different approximations, can account for dynamic and static electron correlation. Second, we want to gain insight for which materials and dopants electron correlation becomes important and, given a certain degree of electron correlation, which method suffices to capture it.
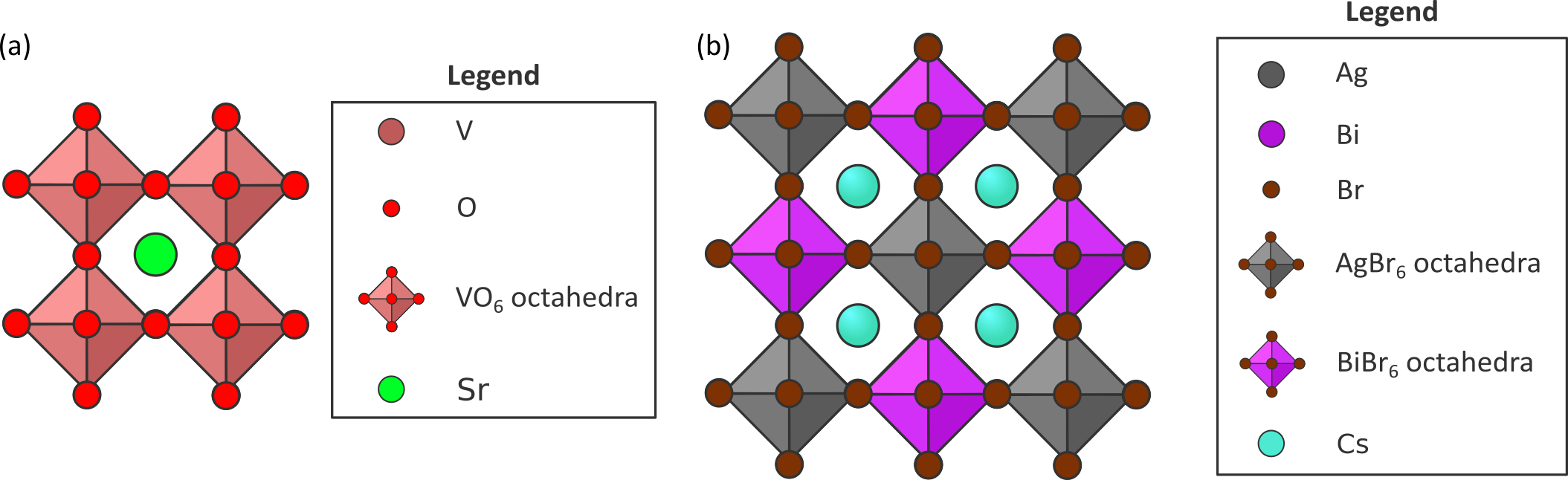
Figure 2: Depiction of two perovskite materials: (a) SrVO3 and (b) Cs2AgBiBr6.
The first material we will investigate in this thesis is the cubic perovskite oxide SrVO3 (see Figure 2a). It is a typical example of a strongly correlated material and a lot of benchmark literature data is available on the accuracy of various many body techniques. Therefore, it will be possible to benchmark different theoretical many-body approaches and compare the obtained results with published theoretical methods and angle-resolved photoemission spectroscopy experiments [4]. Within this thesis topic a collaboration is foreseen with the Quantum Group (Verstraete) who has ample expertise on quantum many-body techniques based on tensor networks. For relatively small systems like SrVO3, very advanced methods such as periodic coupled-cluster calculations or tensor based methods could be benchmarked too to reach quantum accuracy. Following this benchmark study, we will investigate more technologically relevant MHPs, starting with CsSnBr3 and systematically increasing the complexity. First, we will exchange Sn for Pb, for which relativistic effects have to be taken into account due to its higher mass. Afterwards, we will exchange Cs+ for the larger and more dynamic methylammonium ion. Finally, we will investigate double perovskites, for which the B cations (Sn2+ or Pb2+) are replaced with two different metals, such as Ag+ and Bi3+, yielding Cs2AgBiBr6 (see Figure 2b). These double perovskites are of particular interest because they show great potential for photovoltaic applications [5]. Moreover, doping these structures with a rare-earth element such as Eu en Er leads to increased charge carrier mobilities. Therefore, our final goal will be to investigate the effect of doping on the electronic properties of Cs2AgBiBr6.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]Keywordsstrongly correlated systems, many-body techniques, metal halide perovskites, electronic structure, static electron correlation, dynamic electron correlationReferences
[1] Morgante et al., Int. J. Quantum Chem. 120, 26332 (2020)
[2] Steele et al., Science 365, 679-684 (2019)
[3] Golze et al., Front. Chem. 7, 377(2019)
[4] Wadati et al., Phase Transit. 79, 617-635 (2006)
[5] Keshavarz et al., Adv. Mater. 32, 2001878 (2020)
