Background and problem

In principle, the Schrödinger equation allows us to fully predict a system’s multidimensional wavefunction and behavior. However, solving this equation exactly is not trivial and even impossible for realistic materials containing more than a handful degrees of freedom. Density functional theory (DFT), in which the 3D electron density is the central quantity instead of the multidimensional wavefunction, is therefore the most popular quantum mechanical approach in solid state science nowadays. However, the accuracy of a DFT calculation strongly depends on which of the many available exchange-correlation functionals is chosen.1 Furthermore, the currently available functionals all fail in the case of systems exhibiting strong electron correlation. This typically occurs when electrons become localized, density fluctuations vary widely over the system, and bands crossing the Fermi energy have a narrow bandwidth. This is the case, for instance, in transition metal-compounds, rare-earth compounds, and organic conductors. Strong electron correlation should therefore be taken into account by using higher-level simulation techniques, such as the random phase approximation (RPA) or wavefunction based tensor networks. The latter method however come at a higher computational cost, therefore a viable strategy consists in constructing effective Hamiltonians, where higher accuracy calculations are conducted in a lower dimensional space  made of the specific electronic bands that are responsible for the strong electron correlations.   This hybrid approach relies on the computational efficiency of DFT and combines it with more accurate methods for those states that are responsible for strong electron correlations.  A key question is the construction of the effective Hamiltonians for the problematic electron bands.2 The strategy that will be adopted here is to start from the DFT calculations, isolate the bands that are close to the Fermi level and construct maximally localized Wannier functions, which are a set of real-space localized orbitals forming the real-space counterpart of Block orbitals.2,3 They have the advantage that they span precisely the required energy range and that they naturally incorporate hybridization and bonding appropriate to their local environment. Using Wannier functions, the effective systems, with substantially fewer degrees of freedom, can be simulated at a higher level of theory, whereas the other bands are still treated with DFT.

Goal

In this thesis, it our aim to develop a methodology to construct the effective Hamiltonians that are able to treat the electron correlations with higher accuracy.  To this end we will design a hybrid RPA/DFT or tensor/DFT scheme to increase the accuracy of quantum-mechanical simulations for technologically important materials which are prone to strong electron correlation. To this end, first the electron bands of the systems will be calculated via DFT and the relevant bands around the Fermi level that need to be considered in the effective Hamiltonian will be selected. These bands should be isolated and should be transformed to maximally localized Wannier functions. These Wannier orbitals then define the low-energy subspace of interest from which in the second stage of this thesis the hopping amplitudes and interaction terms will be computed at the RPA level of theory. Alternatively the effective Hamiltonian in the reduced subspace may be treated using other tensor networks methods, that are being developed within the Quantum Group of Prof. Verstraete.  Such hybrid DFT/RPA or DFT/tensor based models show a lot of potential to reach unprecedented accuracy for systems showing strong electron correlations. 

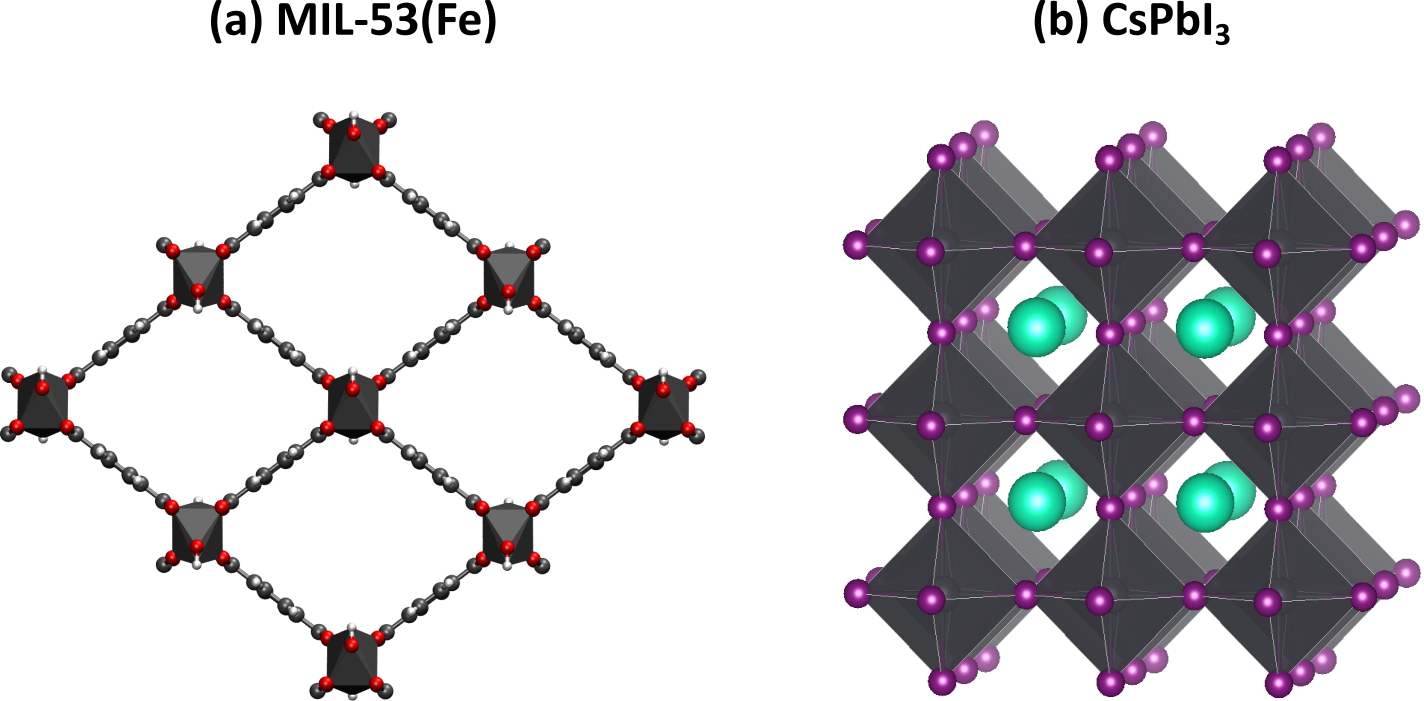
Figure 1: Atomic structure of MIL-53(Fe) and CsPbI3, the two materials showing strong electron correlation investigated in this thesis.

Two specific systems featuring strong electron correlation will be investigated in this thesis, both shown in the figure. At first instance, you will use the hybrid RPA/DFT scheme to determine accurate ground state energies of the metastable phases of the flexible metal-organic framework MIL-53(Fe).4 This material can undergo a phase transition between a closed and an open pore phase. Therefore, it can potentially be used in sensing, gas storage, and separation applications. To correctly predict under which conditions it is able to breath, the energies of the different phases should be determined with an error that is as low as possible. DFT fails in this regard, because the presence of various possible spin configurations has a large impact on the electron properties.

A second system of interest in this thesis proposal is the metal halide perovskite CsPbI3.5 This material shows strong light absorption, long charge carrier lifetimes, and high carrier mobility, which makes it very interesting for various optical applications such as solar panels and medical scanners. DFT typically fails to determine accurate band gaps of perovskites. As a result, most simulations on this system have been performed at a very high level of theory with high computational cost. By using the hybrid RPA/DFT scheme, the computational load to determine accurate electron band schemes could be severely reduced, allowing us to consider larger perovskite systems and account for the experimental doping of this system.

This thesis relies on a collaboration between the Center for Molecular Modeling (Van Speybroeck) having ample expertise in the properties of technologically important materials and their simulation with Density Functional Theory Methods and the Quantum Group (Verstraete) having ample expertise in tensor networks and the theory of quantum entanglement and it application to condensed matter systems.  The potential student for this topic should have interest in fundamental aspects of quantum simulations and their application to important materials for engineering applications.