Extracting high-dimensional free energy surfaces from molecular simulations to accurately estimate the rate of physical and chemical processes
Extracting high-dimensional free energy surfaces from molecular simulations to accurately estimate the rate of physical and chemical processes
Promotor(en): L. Vanduyfhuys, V. Van Speybroeck /28198 / Model and software developmentBackground and problem
Molecular modeling is a hybrid field of science combining chemistry and physics, in which scientist try to understand and predict the behavior of molecules and materials by modeling interactions between particles at the molecular scale. Typically, two very different length (and time) scales have to be considered: on one hand, we want to understand and predict the macroscopic behavior of the system (e.g. how much does steel expand when heating it up) or reaction (e.g. how fast are nitrogen oxides converted to harmless molecular nitrogen in the catalytic converter of a car). On the other hand, the physical models implemented in the computer simulations describe interactions at the microscopic scale (e.g. the coulomb interaction between electrons and nuclei). Bridging the molecular interactions and the thermodynamic observables is not a trivial task and is the subject of statistical physics [1]. This is done by introducing the concept of an ensemble of identical systems that satisfy macroscopic boundary conditions (e.g. given pressure, temperature, …) and defining their corresponding partition function. This partition function is computed from the microscopic degrees of freedom of the system and allows to extract the thermodynamic potential, that is the free energy. Unfortunately, computer simulations such as molecular dynamics (which starts from the Born-Oppenheimer approximation and treats the dynamics of the nuclei using Newton’s equations of motion) do not allow to directly extract the partition function itself. Instead, using the ergodic principle, one can extract thermal ensemble averages. In case of the canonical ensemble, these averages take the form:
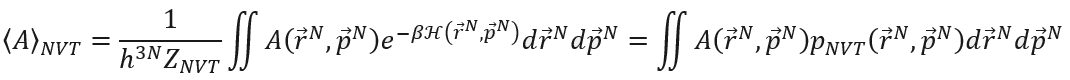
The thermal average NVT is expressed as an average of the corresponding microscopic observable A over the entire phase space, weighted by the ensemble-specific probability distribution pNVT. While the free energy cannot be directly expressed as such a thermal average, one can still extract differences and/or derivatives of free energies.
A further complication arises from the finite timescale achievable during the simulations, which leads to the impossibility of properly sampling the entire phase space. Consider for example a system whose phase space consists of two regions with high probability separated by a narrow region with very low probability (i.e. a barrier). This is typically the case for activated process in physics (e.g. phase transitions) and chemistry (e.g. chemical reactions). If one would initialize the system in one of the high-probability regions and run a regular molecular dynamics simulation, the system would never cross the low probability barrier towards the second region on the timescales that are currently accessible in normal simulations (hundreds of ps to a few ns). In terms of the thermodynamic potential (e.g. the Helmholtz free energy), the two regions correspond to a low free energy, while the narrow barrier in between corresponds to a high free energy barrier that the system is not able to cross easily. Therefore, one needs enhanced sampling simulations [2] such as metadynamics or umbrella sampling, in which the system is biased along a certain degree of freedom – denoted as the collective variable – that is able to describe the transition between the two high probability regions. In this way, the free energy of the process can be retrieved as function of the collective variable (Figure 1, left) [3]. Finally, the rate at which the process occurs can be obtained from the free energy profile using transition state theory. Such rate is a macroscopic quantity that can be directly measured, closing the gap between theory and experiment.
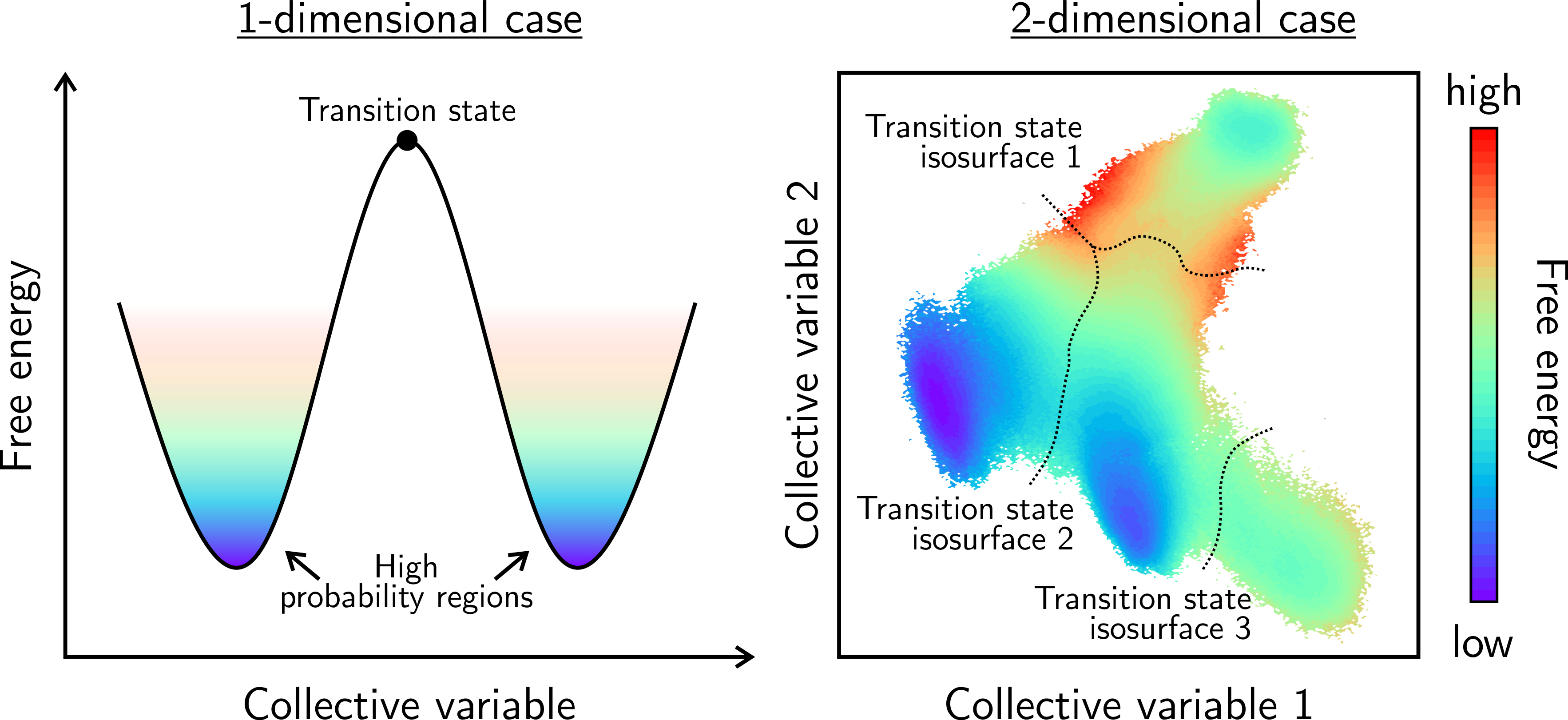
Figure 1: Illustration of the free energy surface for a process that can be characterized with (left) one collective variable and (right) two collective variables. The regions of high probability (purple) correspond to low free energy and can be interpreted as (meta)stable states. The transition state, representing a local maximum in the free energy, corresponds to a single point in the 1D profile or a line/path on the 2D profile.
The procedure outlined above has already been tested and validated for processes that can be characterized by a single and ‘simple’ collective variable (e.g. the distance between two atoms). However, if two independent collective variables are required to distinguish between all relevant regions of phase space (Figure 1, right), there are still some fundamental issues that need to be solved. The most prominent one is the definition of a transition state isosurface, that outlines the boundary between various thermodynamically stable macrostates, and the subsequent extraction of the corresponding process rate.
Goal
In this master thesis, the student will explore the extraction of reliable reaction rates from multidimensional free energy surfaces (FESs), further expanding the scope and use of our in-house developed ThermoLib library [4]. The student will be faced with the challenging task of deriving an appropriate theoretical framework to treat transition state surfaces in higher dimensions and to extract the required data from molecular simulations. Next, such framework will need to be implemented in ThermoLib as an integrant part of the package. The testing will be done by applying it to various relevant physical processes and chemical reactions that are currently under investigation at the CMM, spanning from diffusion of small molecules in microporous materials to catalytic reactions commonly used in the petrochemical industry. Despite the desire to tackle problems with low-dimensional collective variables, it is often encountered that crucial reaction steps are inherently multidimensional in nature and hence require more than two collective variables to describe a single conversion process. Therefore, two or more degrees of freedom are often ‘squeezed’ in a single linear combination of coordination numbers to reduce the final dimensionality of the FES. Alternatively, some parts of the reaction/process are assumed to be fast, and no CV is used to biased them. In the final part of the thesis, the student will then also test how these choices impact the computed rate constants by considering complex free energy surfaces, for which the currently available 1-dimensional implementation is insufficient.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]Keywordsfree energy surface, Molecular simulation, phase space, Statistical physics, process rate, Transition state theoryReferences
[1] D. Frenkel and B. Smit, “Understanding Molecular Simulation”, Academic Press, 2002, San Diego
[2] R. Demuynck et al., J. Chem. Theory Comput., 2017, 13(12), 5861
[3] R. Demuynck et al., J. Chem. Theory Comput., 2018, 14(11), 5511
