Background and problem

Molecular modeling is a hybrid field of science combining chemistry and physics in which scientist try to understand and predict the behavior of molecules and materials using computer simulations that model the interactions between various particles at the molecular scale. It is important, however, to understand that this field involves two different length (and time) scales. On one hand we want to understand and predict the macroscopic behavior of the system (e.g. how much does steel expand when heating it up) or reaction (e.g. how fast are nitrogen oxides converted to harmless molecular nitrogen in the catalytic converter of a car). On the other hand, the physical models implemented in the computer simulations describe interactions at the microscopic scale (e.g. the coulomb interaction between electrons and nuclei). Making the bridge between the molecular interactions and the thermodynamic observables is not a trivial task and is the subject of statistical physics [1]. This is done by introducing the concept of an ensemble of identical systems that satisfy macroscopic boundary conditions (e.g. given pressure, temperature, …) and defining the corresponding partition function. This partition function is computed from the microscopic degrees of freedom and allows to extract the thermodynamic potential (e.g. free energy). Unfortunately, computer simulations such as molecular dynamics (which starts from the Born-Oppenheimer approximation and treats the dynamics of the nuclei using Newton’s equations of motion) do not allow to directly extract the partition function itself. Instead, using the ergodic principle one can only directly extract so-called thermal ensemble averages. In case of the canonical ensemble, these averages take the form:

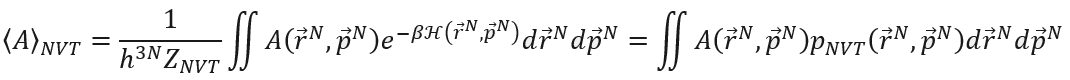
The thermal average <A> is expressed as an average of the corresponding microscopic observable A over entire phase space weighted by the ensemble-specific probability distribution p. Unfortunately, as the free energy cannot be expressed as such a thermal average, one can only extract differences or derivatives of free energies. Furthermore, as computer resources are finite, simulations do not allow to sample the entire phase space. Consider for example a system whose phase space consists of two regions with high probability that are separated by a narrow region with a very low probability (i.e. a barrier). This is typically the case for activated process in physics (e.g. phase transformations) and chemistry (e.g. chemical reactions). If one would initialize the system in one of the high-probability regions and run a regular molecular dynamics simulation, the system would never cross the low probability barrier towards the second region on the timescales that are currently accessible in molecular dynamics simulations. In terms of the thermodynamic potential (e.g. the Helmholtz free energy), the two regions correspond to a low free energy but the narrow barrier in between corresponds to a high free energy the system is not able to cross easily. These types of processes are also denoted as rare events, as the high free energy barrier implies that the transition rarely happens on the time scale of regular molecular simulations. Therefore, one needs enhanced simulations [2] (such as metadynamics or umbrella sampling) in which the system is explicitly driven in the direction of the process (characterized by a certain degree of freedom denoted as the collective variable) to perform the transition. These advanced simulations allow to extract the free energy as function of the collective variable (see figure below) to characterize the thermodynamic stability in terms of the chosen collective variable [3]. Finally, the application of transition state theory then allows to compute the transition rate, i.e. the rate at which the process occurs. When the process under study represents a molecular system undergoing a chemical reaction, one can extract the chemical reaction rate and compare directly with experimental results.

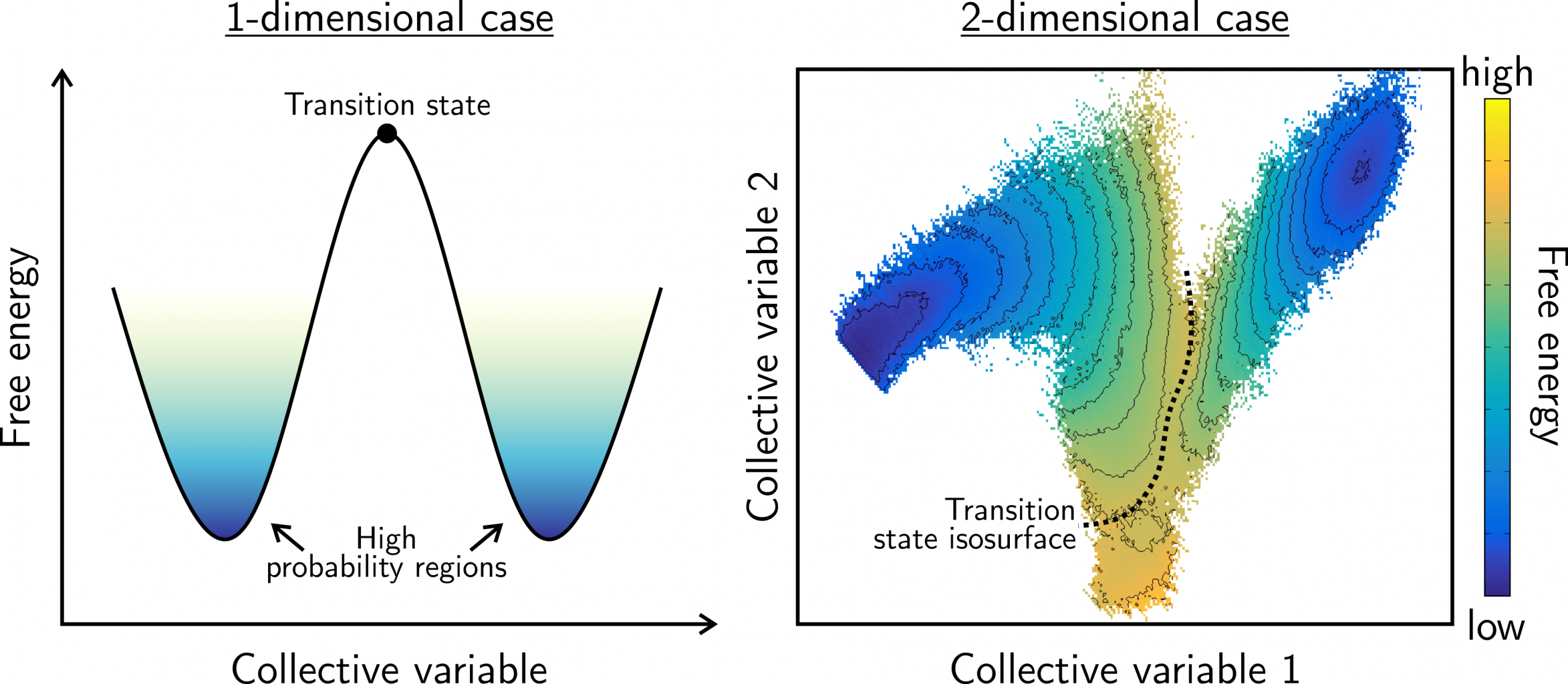
Figure 1: Illustration of the free energy surface for a process that can be characterized with (left) one collective variable and (right) two collective variables. The regions of high probability (blue) correspond to low free energy and can be interpreted as (meta)stable states. The transition state, representing a local maximum in the free energy, corresponds to a single point in the 1D profile or a line/path on the 2D profile.

The procedure outlined above has already been validated for processes that can be characterized by a single and ‘simple’ collective variable (e.g. the distance between two atoms or the coordination number of a certain bond). However, whenever the process is inherently two dimensional, i.e. two independent collective variables are required to distinguish between all relevant regions of phase space, there are still some fundamental issues that need to be solved. The most prominent of which is the definition of a so-called transition state that defines the boundary between various thermodynamically stable macrostates and how to extract the corresponding process rate. Furthermore, as a result of the finite computational resources, any molecular simulation is always hampered by two related issues: (1) did the simulation access all relevant regions of phase space and (2) did they accurately sample those regions? Both are related to the convergence and accuracy of the simulation and can be addressed by an adequate error estimation on the extracted free energy profiles.

Goal

In this thesis, the student will first focus on a consistent implementation (in a Python package) of the aforementioned methodology for extracting free energy profiles from molecular simulations output as well estimating kinetic transition rates based on transition state theory. Next, the student will extend the methodology towards 2 dimensional free energy surfaces and perform the required implementation and testing. This implementation will be tested by applying it to various relevant chemical reactions that are currently under investigation at the CMM. In particular, the conversion of relatively simple biomass-derived organic molecules both in hot liquid water and in a zeolite catalyst (in the context of producing sustainable chemicals from renewable resources) is being studied with enhanced sampling techniques. Despite the desire to tackle problems with low-dimensional collective variables, it is often encountered that crucial reaction steps are inherently multidimensional in nature and hence require multiple collective variables to describe a single conversion process. Therefore, both theory and software should be extended to cope with these processes, in order to allow for an accurate comparison between computational models and experiments. Hence in a second stage, the student will  investigate a further generalization towards higher dimensions. Finally, we also envision to pursue a consistent quantification and propagation of errors to allow to determine whether the performed molecular simulations are well converged. Depending on the interest of the student, the focus can be shifted towards the implementation aspect, the development of a general methodology in N dimensions or the error estimation.

This topic involves the application of the theory of statistical physics to derive extensions of the models towards higher dimensions, application of the theory of statistics and probability to estimate errors as well as the implementation of the these aforementioned features in existing Python packages.