Many properties of matter can be simulated and understood at the nanoscale, by directly solving the electronic wavefunction in the field of the nuclei. An exact solution of the electronic problem from first principles has an exponential-scaling computational cost and is only feasible for systems counting up to 40 electrons. However, in many disciplines that employ molecular simulations, one is interested in macromolecular systems counting 10⁵ or more electrons, e.g. when simulating an entire protein or a cell membrane. (See Fig. 1.) In such scenarios, one typically uses force-field models, in which electrons are not treated explicitly. Only effective interatomic interactions are computed, and due to a lack of physically sound approximations, one usually employs very empirical models.

Figure 1. The cross section of a cell membrane from a molecular dynamics simulation.

A fundamental limitation of force fields is the absence of a clear relation to a quantum-mechanical electronic-structure theory. Because most force-field models are constructed ad hoc, using intuition and educated guesses, it is impossible to gradually improve their accuracy by bringing them conceptually closer to an electronic-structure theory.

In conventional force fields, the only explicit particles are "atoms". Each atom represents a nucleus and a fractional number of electrons bound to it. All other electronic degrees of freedom, i.e. the large majority, are thus discarded. In this thesis, explicit electron force fields (EEFFs) will be investigated, which describe the electronic structure in more detail, through the average positions of each electron (pair). Existing EEFFs have followed the traditional route of empiricism and educated guesses, [1,2] which is a missed opportunity. The average electron positions were never compared to ab initio data, which will be the main novelty in this thesis. The theoretical foundation for this comparison is the Modern Theory of Polarization, [3] which defines so-called Wannier or Foster-Boys maximally localized orbitals. The centers of these localized orbitals, see e.g. Fig. 2, can be interpreted as average positions of electron (pair) clouds. For example, the molecular dipole moment can be computed from the positions and charges of the nuclei and the Foster-Boys centers.

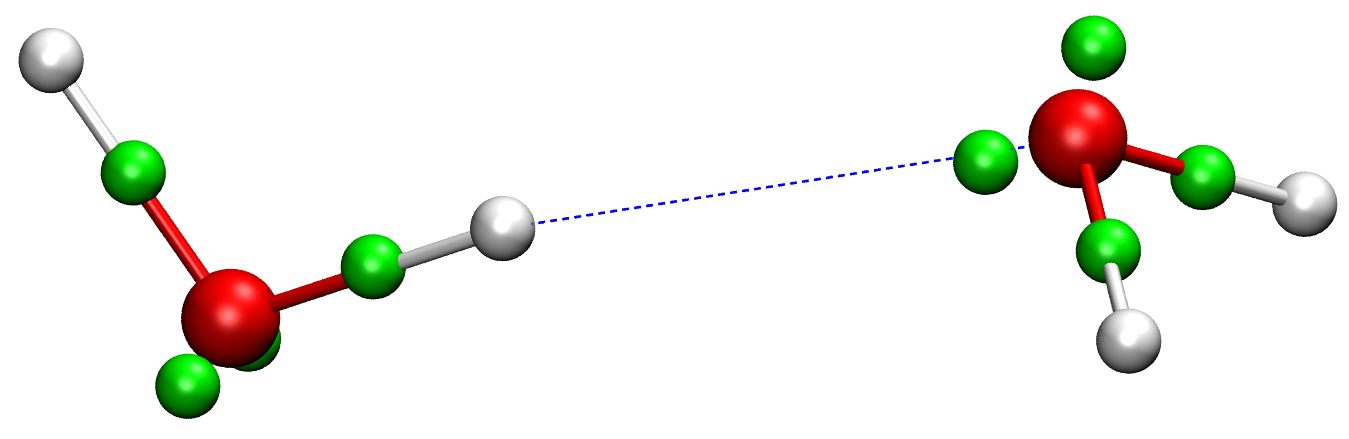
Figure 2. Foster-Boys centers (green spheres) in a water dimer (oxygen=red, hydrogen=white).

Localized orbitals are a specific unitary transformation of the Kohn-Sham orbitals in DFT, and hence incur no loss of information, all observables are still accessible. However, to arrive at a computationally efficient EEFF, a reduction in complexity is needed, e.g. by only retaining essential properties of the localized orbitals, in such a way that the most relevant observables (e.g. energy and electrostatic multipole moments) can still be estimated to good accuracy. The central goal of this thesis is to investigate which types of reductions (i) still allow one to apply the variational principle and (ii) to perform reliable and efficient molecular dynamics simulations for relevant test cases, e.g. proton diffusion in liquid water. These insights will be used to develop an EEFF, in which physical approximations and machine learning (SchNet [4]) can be combined.

[1] J. T. Su & W. A. Goddard. Phys. Rev. Lett. 99, 185003 (2007). http://link.aps.org/doi/10.1103/PhysRevLett.99.185003

[2] J. Herzfeld & S. Ekesan. Phys. Chem. Chem. Phys. 2, 30748–30753 (2016). http://xlink.rsc.org/?DOI=C6CP06100A

[3] R. Resta & D. Vanderbilt. in Physics of Ferroelectrics 105, 31–68 (Springer Berlin Heidelberg, 2007). http://link.springer.com/10.1007/978-3-540-34591-6_2

[4] K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko, and K.-R. Müller. J. Chem. Phys. 148, 241722 (2018). https://aip.scitation.org/doi/10.1063/1.5019779