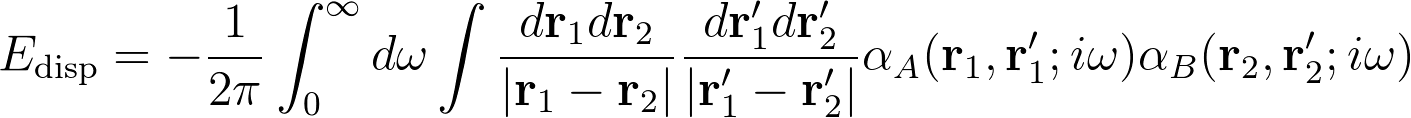Dispersion models with an explicit treatment of monopolar density fluctuations
Dispersion models with an explicit treatment of monopolar density fluctuations
Promotor(en): T. Verstraelen, D. Van Neck /17MODEV06 / Model and software development, Many-particle physicsThe dispersion interaction is a weak (but omnipresent) force between molecules due to correlated zero-point motion of electrons in the different molecules. The classical example of dispersion forces in nature is the gecko climbing on smooth surfaces like glass windows. Dispersion forces between the gecko toe pads, see Fig. 1, and a smooth surface are strong enough to carry the weight of the animal.
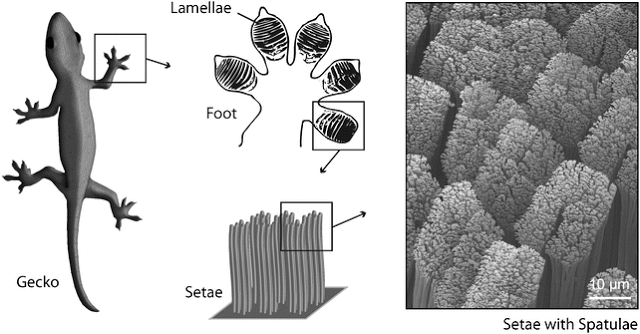
Fig. 1. Anatomy of the gecko toe pad.Dispersion interactions are also of critical importance in various molecular simulations, especially when dealing with extended systems (thousands of atoms). The first quantum mechanical description is due to London, who showed that the leading term in the dispersion interaction between two hydrogenic atoms is attractive and proportional to R^{-6}, where R is the internuclear distance. In the more general case, the second-order dispersion interaction between two molecules, A and B, can be computed with a generalized Casimir-Polder expression:
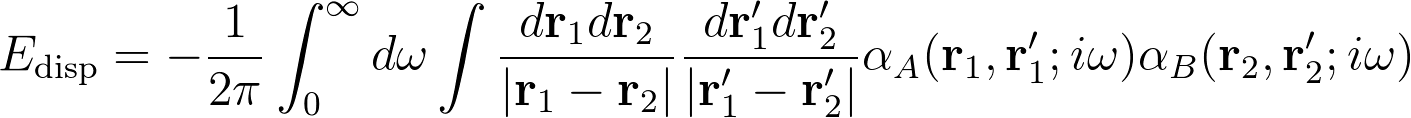
where alpha_A and alpha_B are the frequency dependent response functions of the two molecules. A direct evaluation of the Casimir Polder expression for an extended system is computationally infeasible.
Most popular (approximate and computationally cheap) dispersion models start from the assumption that the frequency-dependent response kernel can be written as a set of (non)interacting atomic inducible dipoles. In the simplest case, this leads to a model for the dispersion energy, which is a sum over all atom pairs, where each term has the London form: C_{ij,6} R_{ij}^{-6}. The parameter C_{ij,6} depends on the linear response properties of atoms i and j.Goal
In this thesis, we will not rely on the popular assumption that molecular linear response is a sum of local atomic polarizabilities. Instead density-fluctuations, involving exchange of electrons between atoms, will be included explicitly. The central question in this thesis is: "What is the impact of these non-local fluctuations on the dispersion interaction?" For some model systems, this has been studied already, e.g. the dispersion between parallel atomic wires falls of with R^{-3} [Misquitta2014] The implications on interactions between more mundane molecules, e.g. molecular dimers in the S66 set, remains unclear.
In this thesis, dispersion interactions will be modeled with the adiabatic connection fluctuation dissipation (ACFD) theorem. This is an elegant quantum-mechanical theory, which is widely used to model electron correlation effects in terms in terms of the frequency-dependent electronic linear response. It was shown that approximate linear response models already yield reasonable estimates of the correlation energy, especially the dispersion interaction. For example, the random-phase approximation (RPA) of the electronic linear response is currently extensively studied for this purpose. One may even derive an RPA equivalent of the Casimir-Polder expression.
Response functions will be computed with the adiabatic approximation in time-dependent density functional theory (TD-DFT). A new implementation will be developed during the thesis, building on the Kohn-Sham inversion method proposed by Staroverov group. [Kohut2014] With this inversion technique, the non-interacting response function can easily separated from the electron-electron interactions in Hybrid TD-DFT calculations, providing more insight into the structure of the response function.
Mobility: This thesis fits well in a new collaboration with Alexandre Tkatchenko (Luxembourg), who is an expert on many-body dispersion corrections for DFT calculations. A short visit to his group could be valuable to analyse the results of this thesis.
Motivation Appl. Phys.: The computation of dispersion interactions require a fundamental understanding of the quantum-mechanical electronic structure of molecules. The results of this thesis are directly relevant for applied computational research in materials science and chemistry.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) NANO, MODELLING, FUNDAMENTALSKeywordsquantum-mechanical electronic structure theory, excited states, dispersion interactions, time-dependent density functional theoryReferences
[Misquitta2014] http://dx.doi.org/10.1103/PhysRevB.89.045140
[Kohut2014] http://dx.doi.org/10.1063/1.4871500