Disentangling the transition metal dimers
Disentangling the transition metal dimers
Promotor(en): D. Van Neck, V. Van Speybroeck /16FUND04 / Many-particle physicsSince the 1930s, the quantum theory of molecular electronic structure is completely known. However, due to the exponential increase of the Hilbert space with system size, practical approximate computational methods are needed. For certain classes of molecules, typically when π-conjugation or transition metals come into play, Hartree-Fock theory fails completely. A multi-reference description based on several important Slater determinants is required to obtain meaningful results. The energy difference between the exact and the Hartree-Fock solution is called the correlation energy and can be divided into two contributions: static and dynamic correlation. Static correlation can be resolved by calculating the electronic structure exactly in the so-called active space. This is a small subset of orbitals relevant to the chemical description of the molecule under study. One can think, for example, about π-conjugated molecules and the set of π-orbitals relevant to describe its resonant Lewis structures. The orbitals in this active space can be optimized with the complete active space self-consistent field (CASSCF) method. In addition to static correlation, an adequate description of dynamic correlation is required as well to obtain accurate potential energy surfaces. Dynamic correlation arises due to the Coulomb repulsion between the electrons in the remaining occupied HF orbitals, which causes small partial occupations in the occupied and virtual orbitals. The most widely used method to calculate dynamic correlation energies for CASSCF wavefunctions is second order perturbation theory (CASPT2), in which a generalized Fock operator is used as zeroth order operator in Rayleigh-Schrödinger perturbation theory.
Explaining experimental data such as bond distances, dissociation energies, harmonic frequencies, anharmonic frequencies, ionization energies, and electron affinities for homo- and heteronuclear transition metal dimers with ab initio quantum chemistry calculations is an extremely hard problem. The minimal active spaces required to obtain meaningful results consist of the 3d, 4s, 4p, and 4d orbitals of both transition metal atoms, or a total active space of 28 orbitals. The electronic structure can be calculated with exact diagonalization in active spaces of up to 16 orbitals. When exact diagonalization is used in CASSCF, the electronic structure of transition metal dimers is not only poorly described due to the limited active space sizes, in many cases it was not even possible to obtain continuous potential energy surfaces. Another method is hence required to study transition metal dimers, and the lack thereof has long impeded the theoretical description of these systems.
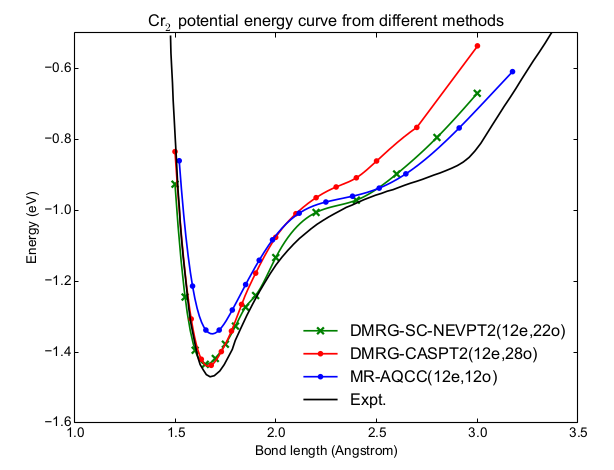
At the Center for Molecular Modeling, a symmetry-adapted high-performance implementation of the density matrix renormalization group (DMRG) was developed, called CheMPS2 [1, 2]. The underlying wavefunction of DMRG is a matrix product state, a low-rank factorization of many-body Hilbert space vectors. This method allows to resolve the electronic structure exactly in complete active spaces of up to 40 electrons in 40 orbitals, and can replace exact diagonalization in the CASSCF (DMRG-SCF) and CASPT2 (DMRG-CASPT2) methods [3]. In 2014 we used DMRG-SCF to provide a better description of the electronic structure of the oxo-Mn(salen) complex, an important industrial catalyst, which is known to be very challenging problem for electronic structure methods [4]. The symmetry-adaptation is ideal to tackle the different potential energy surfaces of transition metal dimers, as they quite often lie in different spin and point group symmetry sectors. In February 2016, we have also added DMRG-CASPT2 to our in-house DMRG code, and we are currently in the process of fine-tuning and benchmarking this method.
Goal
Within this master thesis, you will learn about conventional (CASSCF and CASPT2) and novel (DMRG, DMRG-SCF, DMRG-CASPT2) electronic structure methods for multireference problems and how to use our in-house DMRG code CheMPS2 (which contains the DMRG-SCF and DMRG-CASPT2 methods). You will perform a thorough investigation of the low-lying electronic states of transition metal dimers, and will correlate your findings with experimental data such as bond distances, dissociation energies, harmonic frequencies, anharmonic frequencies, ionization energies, and electron affinities.
Context
The development and application of approximate yet accurate electronic structure methods, for use in a high-performance computing environment, in order to explain observed experimental spectroscopic data, lies at the border between engineering and physics, as skills and concepts from both fields are needed to successfully accomplish the thesis goals.
This research topic will be conducted in the framework of a strong international network and if possible the student will be actively involved in work discussions with collaborative partners.
Advised courses: No particular courses are required, but you need to be (or are willing to become) well-versed in second quantization and group theory.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) FUNDAMENTALS, MODELINGKeywordsMulti-reference electronic structure methods, transition metal dimers, Second quantization, symmetry groupsReferences
[1] S. Wouters, W. Poelmans, P. W. Ayers and D. Van Neck. CheMPS2: a free open-source spin- adapted implementation of the density matrix renormalization group for ab initio quantum chemistry. Computer Physics Communications 185 (6), 1501-1514 (2014), http://dx.doi.org/10.1016/j.cpc.2014.01.019 or http://arxiv.org/abs/1312.2415
[2] S. Wouters, CheMPS2: a spin-adapted implementation of DMRG for ab initio quantum chemistry (2013-2016), https://github.com/sebwouters/chemps2
[3] Y. Kurashige and T. Yanai, Second-order perturbation theory with a density matrix renormalization group self-consistent field reference function: Theory and application to the study of chromium dimer, Journal of Chemical Physics 135, 094104 (2011), http://dx.doi.org/10.1063/1.3629454
[4] S. Wouters, T. Bogaerts, P. Van Der Voort, V. Van Speybroeck and D. Van Neck, Communication: DMRG-SCF study of the singlet, triplet, and quintet states of oxo-Mn(Salen), Journal of Chemical Physics 140, 241103 (2014), http://dx.doi.org/10.1063/1.4885815 or http://arxiv.org/abs/1405.5642

