Background and problem

Polymers are macromolecules composed of well-defined monomeric subunits which are the main building blocks of many ubiquitous materials. Because of this chain-like nature one often refers to polymers as polymer(ic) chains. Polymers can be both of natural (e.g. cellulose, latex) or synthetic (e.g. polyvinyl chloride ‘PVC’, polyethylene terephthalate ‘PET’) origin. Due to their mutual interactions, polymer chains of different size and range interweave and form amorphous structures whose complexity depends on different parameters, including their mutual linkage pattern (cross-linking) and the rigidity or softness of their monomeric units.

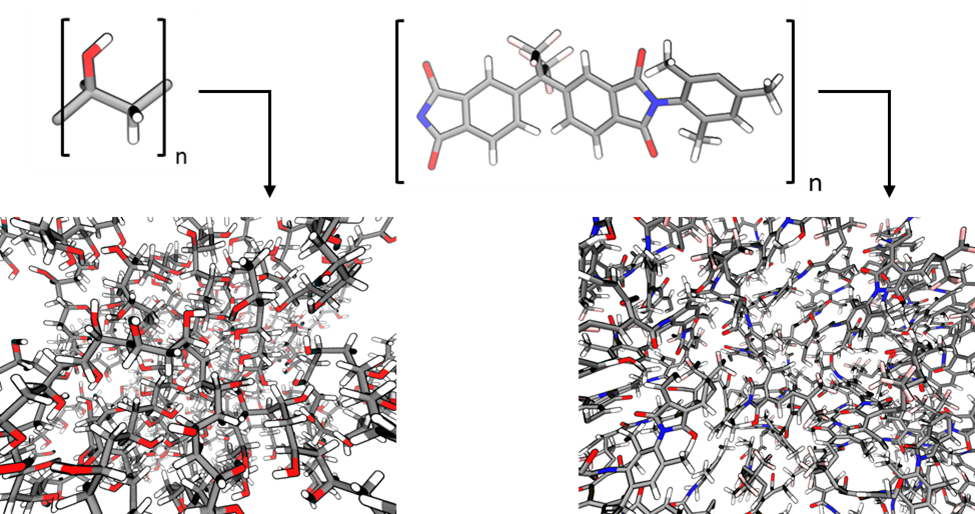
Figure 1. Molecular models of soft (e.g. PVA, left) and rigid (e.g. 6FDA-DAM) polymeric structures coming and their respective monomeric units.

Understanding the microstructure of polymeric materials is of great importance for multiple applications, including drug delivery and gas separation. Molecular modeling and simulation tools are of particular relevance for this end since they grant a molecular-scale comprehensive overview of polymeric microstructures and provide significant insights for the rational design of high-performance polymers. However, one of the main problems for computational modeling of polymers comes from the multiple possibilities in which polymers may arrange themselves. For instance, polymers can be formed from more than one monomeric unit or can be connected in complex intricate networks. Different computational alternatives have been proposed to tackle this challenge, including (i) the stochastic distribution and linkage of monomers[1], and (ii) the implementation of successive linkage/energy minimization cycles.[2]

Considering the multitude of molecular models conceivable for representing polymeric networks, one needs to employ representative parameters capable of relating these models to experiments. One of these parameters is the glass transition temperature, defined by the temperature in which a polymer undergoes a transition from a hard and brittle state, i.e. a so-called glass state, to a viscous rubbery state. In the context of thermodynamic phase transitions, the glass transition is considered to be of a second order, meaning that it is characterized by a discontinuity of second-order derivatives of the thermodynamic free energy, such as heat capacity, bulk modulus and thermal expansion coefficient and is a key engineering feature determining the application range of various polymeric materials. Other parameters of particular interest are the void fraction and pore size distribution, which demonstrate if a given polymer may accommodate gas molecules. This is of particular importance for gas separation applications, where a mixture of gases of different sizes permeate the polymer phase and is separated according to the inherent polymer porosity.

Computational estimation of void fractions (VF) and pore size distributions (PSD) is rather straightforward [3], computing glass transition temperatures however, is a somewhat more strenuous procedure, highly dependent of the model (i.e. chain lengths, cross-linking degree, monomer distribution) and the simulation setup (i.e. force field model, cooling/heating rates applied). At the CMM, we have successfully implemented a methodology to estimate glass transition temperatures in polymers.[4]

Goal

In this thesis, the student will apply various molecular modeling techniques to obtain representative polymeric structures and compute their corresponding properties such as density, pore size distribution and glass transition temperature. Two polymers will be studied: PVA, a widely-used synthetic polymer with a simple monomer structure[5], as well as PIM-1, a more complex polymer that is of great interest in the context of separation membranes.[6]

For these polymers the student will define, driven by experimental observations, the scope of the polymer features (e.g. cross-linking degree, terminator-initiator units, chain lengths, …) which need to be accounted for in the models and hence in the subsequent polymerization procedure. Such polymerization procedure will be achieved using the Polymatic software (among others) which employs successive linkage/molecular dynamics cycles resulting in an ensemble of structures representative of the polydisperse nature of experimental polymers.[2] These structures will serve as input for a series of molecular dynamics simulations at varying temperatures and pressures in order to achieve a thermodynamic equilibration of the polymer. From these simulations, properties such as the density, void fraction and pore size distribution will be computed and serve as a first validation. Glass transition temperatures will be estimated using molecular dynamics simulations with gradual cooling rates. These computationally-obtained values will be compared with the corresponding experimental measurements.

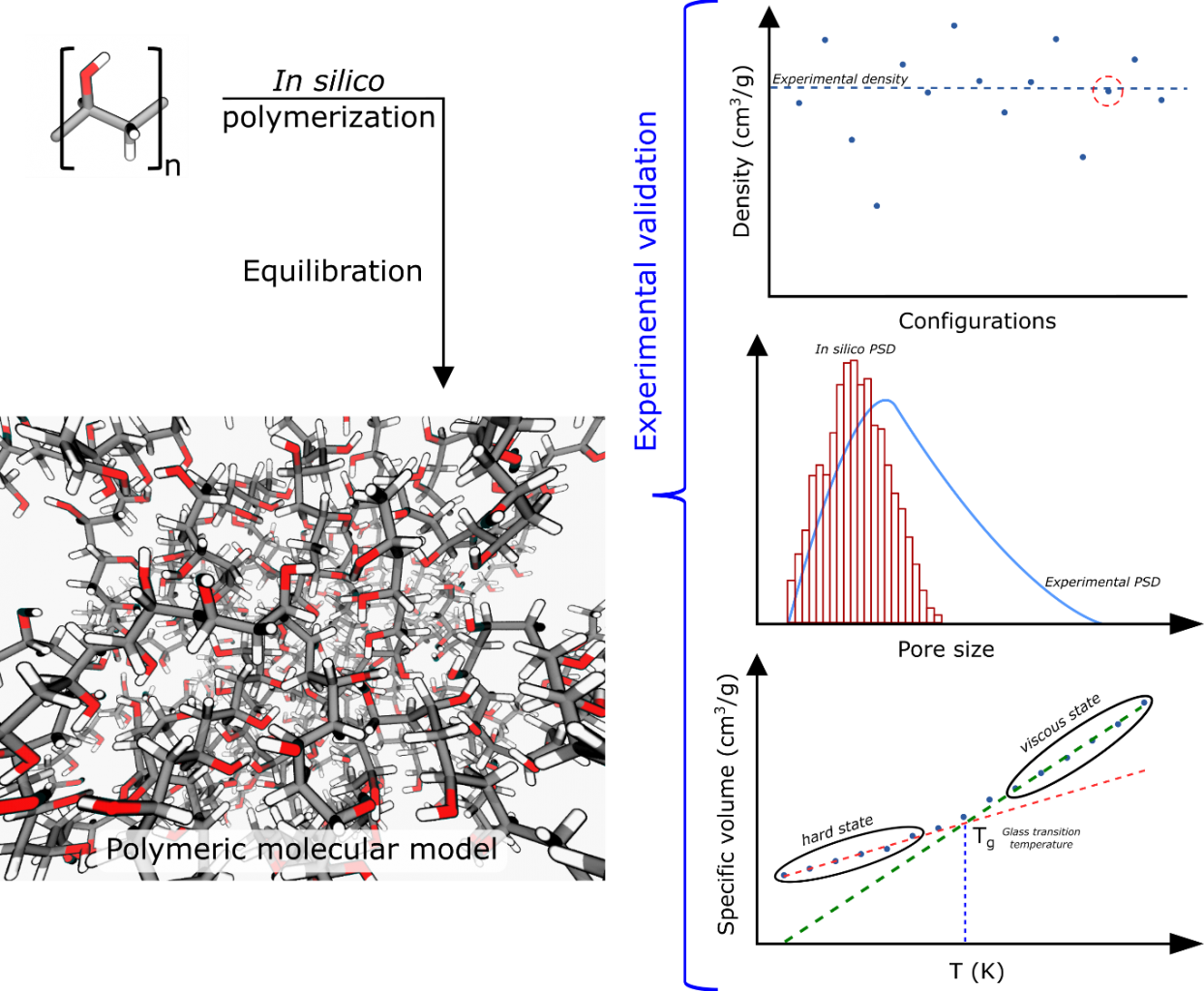
Figure 2. In silico polymerization and validation with respect to experimental values.

Once experimentally-validated equilibrated polymer structures are obtained, they can be used to compute adsorption isotherms via grand canonical Monte Carlo (GCMC). Such additional calculations will assess the affinity of the polymeric membranes towards different gases as well as their potential for thermodynamically-driven gas separation. The topics addressed in this thesis are under the scope of the MOONRISE moonshot project (https://moonshotflanders.be/mot3-moonrise/), an initiative regrouping both academic and industrial researching institutions devoted to the development of highly performing mixed matrix membranes for targeted gas separations.

Remarks

Specialisation "Biomechanics and Biomaterials"