From the atom to the material: The micromechanical model to convert atomic information to macroscopic phenomena
From the atom to the material: The micromechanical model to convert atomic information to macroscopic phenomena
Promotor(en): V. Van Speybroeck, S.M.J. Rogge /20MODEV12 / Model and software developmentProbleemstelling:
Metal-organic frameworks (MOFs) form a versatile and relatively recent class of nanoporous materials that are composed of organic and inorganic building blocks. Due to the wide versatility of molecular interactions present in these materials, varying from strong covalent bonds over coordination bonds to weak dispersion interactions, MOFs exhibit a variety of ‘anomalous’ but highly sought-after cooperative phenomena in response to external stimuli. For instance, some flexible MOFs can undergo large-amplitude phase transitions under the influence of small changes in temperature or pressure and are hence attractive as nanosensing and –actuating materials. However, accurately modelling these materials is not straightforward, as it has become clear that MOFs are not the perfect crystals once envisioned, but rather exhibit inherent spatial disorder in various forms, such as isolated defects and disordered domains (see Figure 1), which strongly impacts the MOF’s performance [1, 2]. One of the grand challenges in computationally modelling MOFs is therefore to combine an accurate description of the atomic-level interactions in these materials with a correct inclusion of spatial disorder. Coarse-grained (CG) models form an attractive pathway to push the length scale that can be computationally modelled beyond a few nanometers – a prerequisite to model correlated disorder [3, 4] – but still fall short of the length scales necessary to model the microsized MOF crystals synthesized experimentally and are often not sufficiently accurate to describe these cooperative phenomena. A fundamentally new CG approach is therefore needed.

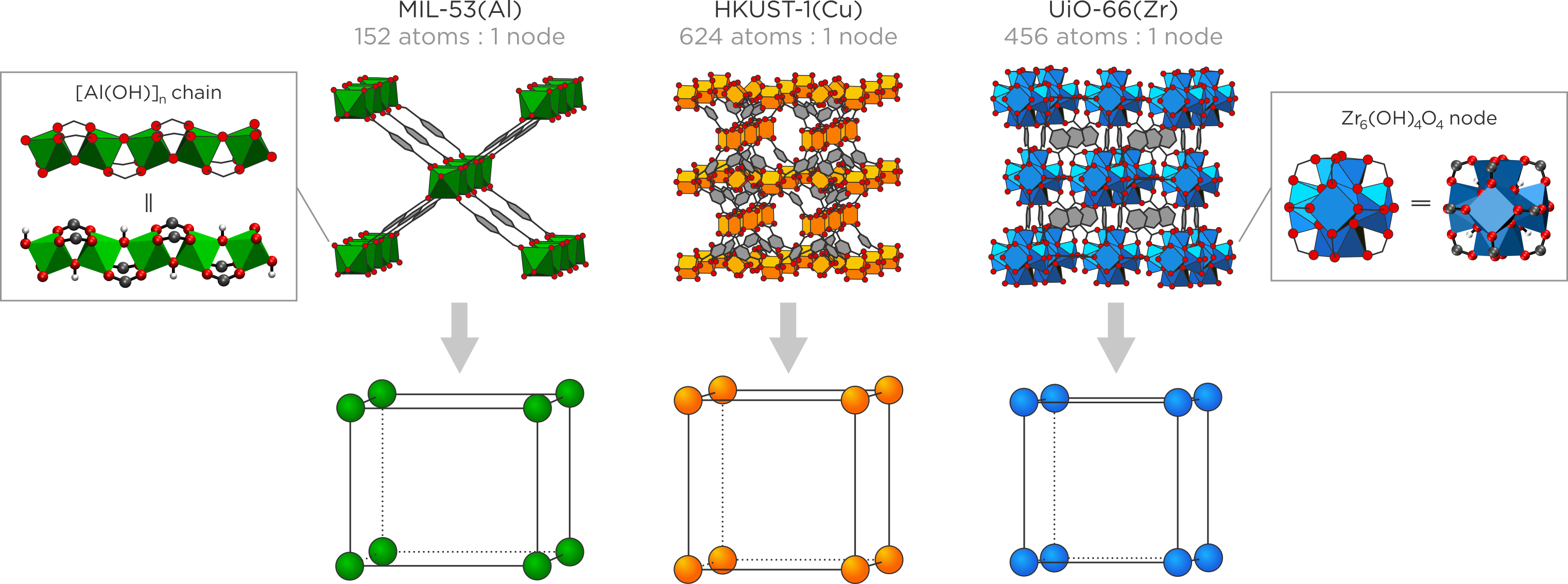
Inspired by this challenge, we very recently introduced the concept of the micromechanical model as a new approach towards coarse-graining framework materials such as MOFs beyond current state-of-the-art CG approaches [4]. The micromechanical model consists of two elements: a systematic mapping procedure to reduce the number of degrees of freedom in the material, by collecting the atoms into so-called CG nodes, and a Hamiltonian description of the dynamics of these CG nodes. The mapping of the micromechanical model, shown in Figure 2, exploits the natural partitioning of these micrometer-sized materials, which cannot yet be modelled, into similar nanosized unit cells. These nanocells typically belong to the same material but exhibit different types of spatial disorder and can be described with conventional ab initio or force field techniques. Such a clear hierarchy allows one to extract atomic-level information at the nanocell level, such as the elastic stiffness tensor, and use this information as input for the micromechanical model to describe micrometer-sized materials. We recently demonstrated that this approach leads to a set of Hamiltonian equations of motion that describe the time propagation of the nodes in the micromechanical model [4]. As it is a very recent model, however, their validity has not yet been extensively tested.
Doelstelling:
In this thesis, it is the aim to implement and validate the micromechanical equations of motion using Python and apply them to study – for the first time – realistic MOF crystals up to the micrometer scale for a variety of interesting systems. This procedure is outlined in Figure 3 for UiO-66, a MOF for which extensive experimental data shows various types of spatial disorder [2]. In a first step of the micromechanical procedure, the mesoscopic material is divided into similar nanocells depending on the spatial disorder present in the nanocell. In the second step, force field simulations are performed to determine their equilibrium cell matrix and stiffness tensor for each of the different nanocell types, indicated with different colors in Figure 3. Finally, these variables are used as input to integrate the nodes of the micromechanical model and predict how the mesoscopic material behaves under operating conditions. Once successful for UiO-66, this procedure can be extended to describe other exciting types of cooperative phenomena, such as the recently discovered phase coexistence in winerack-type structures [5].

The student will be actively coached to make him/her acquainted with the several advanced simulation and coarse-graining techniques early in the thesis year, and to transfer necessary programming skills needed to perform the research. A strong interest in programming is, however, a prerequisite.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]Keywordsmicromechanical model, hierarchical models, Coarse graining, Molecular simulation, Metal-organic frameworks, ImplementationReferences
[1]
I. L. C. Buurmans and B. M. Weckhuysen, "Heterogeneities of individual catalyst particles in space and time as monitored by spectroscopy," Nat. Chem., vol. 4, pp. 873-886, 2012.
[2]
M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, "Correlated defect nanoregions in a metal-organic framework," Nat. Commun., vol. 5, p. 4176, 2014.
[3]
J. P. Dürholt, R. Galvelis and R. Schmid, "Coarse graining of force fields for metal-organic frameworks," Dalton Trans., vol. 45, no. 10, pp. 4370-4379, 2016.
[4]
S. M. J. Rogge, "The micromechanical model to computationally investigate cooperative and correlated phenomena in metal-organic frameworks," Faraday Discuss., 2020. DOI: 10.1039/C9FD00148D.
[5]
S. M. J. Rogge, M. Waroquier and V. Van Speybroeck, “Unraveling the thermodynamic criteria for size-dependent spontaneous phase separation in soft porous crystals,” Nat. Commun., vol. 10, p. 4842, 2019.
