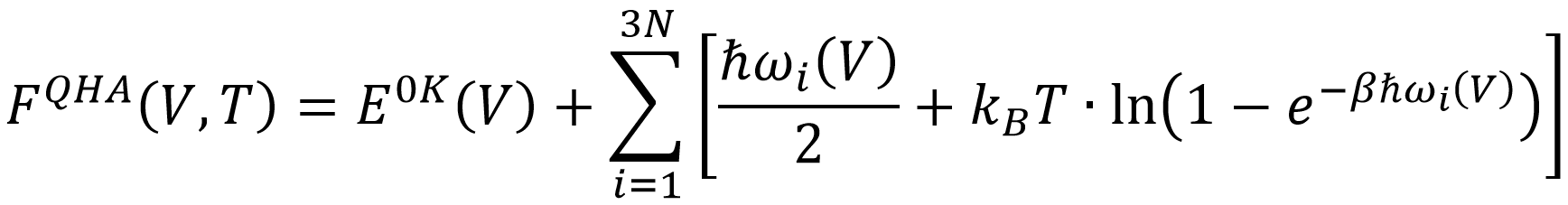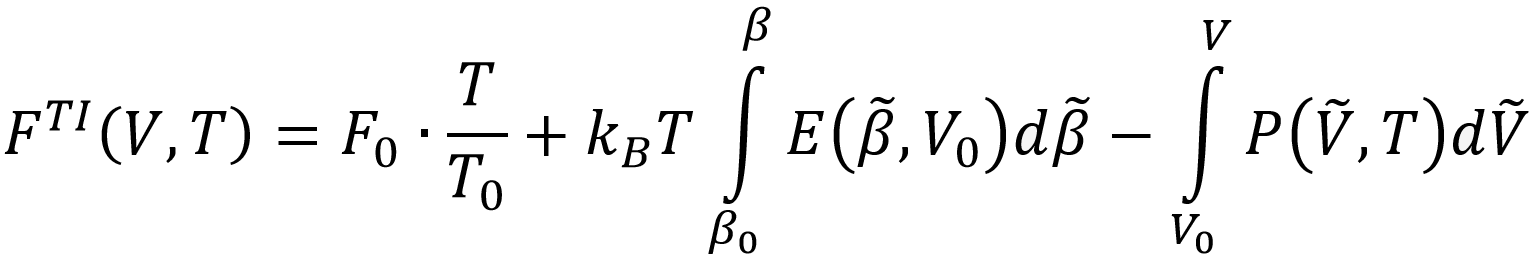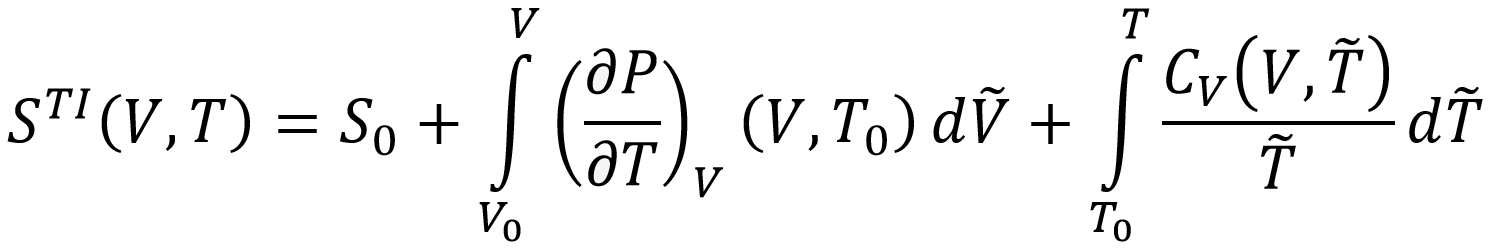Accurate estimation of the temperature-dependent entropy of flexible Metal-Organic Frameworks
Accurate estimation of the temperature-dependent entropy of flexible Metal-Organic Frameworks
Promotor(en): V. Van Speybroeck, L. Vanduyfhuys /18NANO14 / Nanoporous materialsMetal-Organic Frameworks (MOFs) are a class of hybrid nanoporous crystalline materials consisting of inorganic bricks connected to each other by means of organic linkers. Many of these MOFs possess a flexible framework that can transform between various states with large variations in the unit cell volume, which is also denoted as breathing. Two examples of such MOFs are MIL-53(Al), the textbook example of breathing MOFs that can cycle between a large pore and narrow pore state under influence of temperature, and DUT-49(Al), which can absorb large amounts of mechanical energy when subject to high pressures and hence serve as a nano shock absorber. In both cases, the transition between the various states can be modeled once the Helmholtz free energy F is available as function of temperature T and volume V. Furthermore, from the thermodynamic definition F = E - TS, it is clear that an accurate estimate of the temperature dependence of F requires an accurate estimate of the entropy S. Unfortunately, computing the entropy accurately is not a trivial task, which is due to the fact that the entropy cannot be written as a simple ensemble average, as is the case for the internal energy E. Instead, approximations of the potential energy surface (PES) or advanced sampling schemes are required to estimate the entropy.
Goal
In this thesis, various methods will be used to accurately estimate the entropy, and by extension the Helmholtz free energy, of MOFs as function of unit cell volume V and temperature T. The resulting free energy profiles will afterwards be used to investigate the temperature-induced breathing of MIL-53(Al) as well as the mechanical energy storage capacity of DUT-49. A first method that will be considered is the Quasi Harmonic Approximation (QHA) in which the free energy is written as a sum of contributions from 3N uncoupled but volume-dependent harmonic oscillators.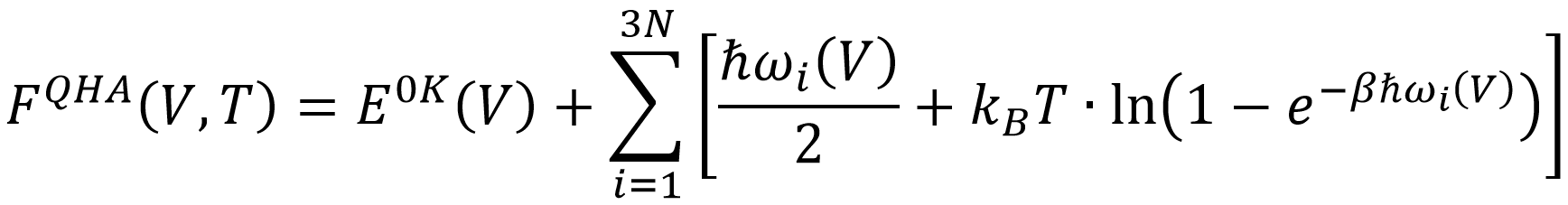
This method includes nuclear quantum effects (NQE) but neglects anharmonicity of the normal modes. A second method uses path-integral molecular dynamics simulations (PI-MD), which extends classical MD simulations to include NQE using the path integral formulation of quantum mechanics, and computes the internal pressure P and energy E as function of V and T to arrive at the free energy by means of thermodynamic integration (TI):
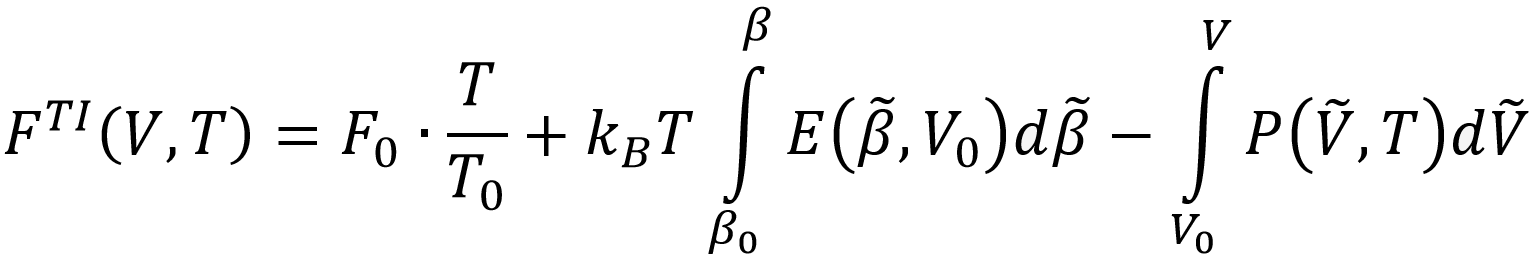
As such, it includes NQE as well as anharmonicity. A third method computes the entropy directly by means of thermodynamic integration of the heat capacity and the thermal derivative of the pressure:
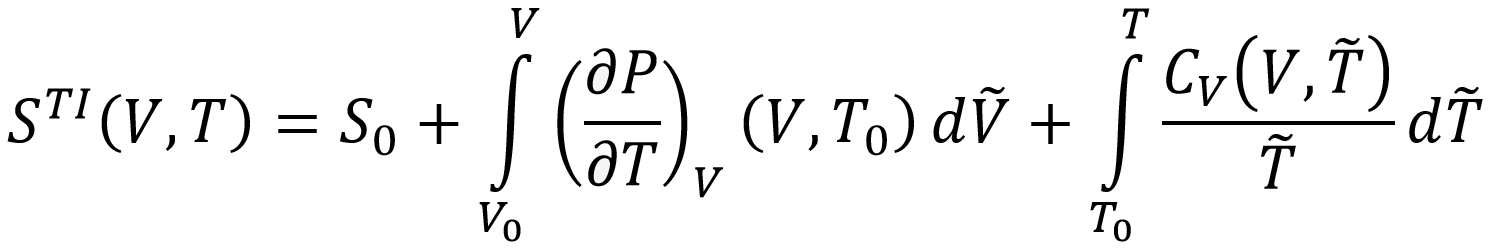
If again PI-MD is used to compute the heat capacity and pressure derivative, NQE and anharmonicity are both taken into account. Finally, by applying and comparing all these methods for MIL-53(Al) and DUT-49, we aim at answering the following questions:
• Is internal energy E and entropy S of MOFs strongly dependent on temperature, or can the Helmholtz free energy be written as F(V,T) = E(V) - T∙S(V)
• How important are NQE and anharmonicity to estimate entropy and internal energy?
• What is the role of entropy in the breathing of MIL-53(Al)? Can the experimental transition temperatures be reproduced?
• How does the energy storage capacity and transition pressure of DUT-49 change as function of temperature?Engineering and physics aspects
Physics: use of advanced thermodynamics and statistical physics
Engineering: investigation of the sensitivity of properties of MOFs towards temperature
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) NANO, MODELINGKeywordsThermodynamics, Statistical physics, entropy, Helmholtz free energy, temperature, anharmonicityRecommended coursesSimulations and Modelling for the Nanoscale