Towards accurate estimates for transition rates of physical transformations in nanoporous crystals
Towards accurate estimates for transition rates of physical transformations in nanoporous crystals
Promotor(en): V. Van Speybroeck, L. Vanduyfhuys /19NANO04 / Model and software development, Nanoporous materialsNanoporous crystals are crystalline materials, i.e. with a long range order, which contain pores or channels on the nanometer scale. Due to their porous nature, they have attracted a lot of attention as promising candidates for various applications in the field of natural gas storage, carbon capture, drug delivery, chemical catalysis, … All of these applications involve physical and/or chemical processes, for which it is crucial to know how fast they progress. The estimation of such rate constants is the subject of transition state theory. Herein, one represents the process in terms of a transition state (TS), which represents an intermediate state in between the initial (I) and final (F) state. In terms of the potential energy surface, the initial and final states are represented by local minima, while the transition state is given by a saddle point, which is a maximum in the direction of the process progression and a minimum in the remaining perpendicular directions. This direction of the process progression plays a crucial role and is quantified by a so-called collective variable (CV), which is a mathematical function of the molecular degrees of freedom (i.e. the atomic positions). In the most simple case, i.e. a system with only 1 degree of freedom which necessarily equals the collective variable, the rate constant can be computed as:

where # represents the difference in energy between the transition state maximum of the E(q) profile and initial state minimum. Although this equation is only valid for 1D systems, it is common to apply it for high-dimensional systems as well, by replacing the energy difference with the difference in free energy. This free energy difference is then estimated from advanced molecular simulations that allow to extract the free energy profile F as function of the collective variable q. However, for many processes, the choice of the collective variable is not unique. Moreover, the resulting free energy profile F(q) can vary drastically when comparing various choices for the collective variable. Using the simple 1D approximation for the rate would then lead to nonsensical results since the process rate is a measurable observable that should be independent on the choice of its microscopical description.
Goal
In this thesis we will start from the more generally valid expression from transition state theory:
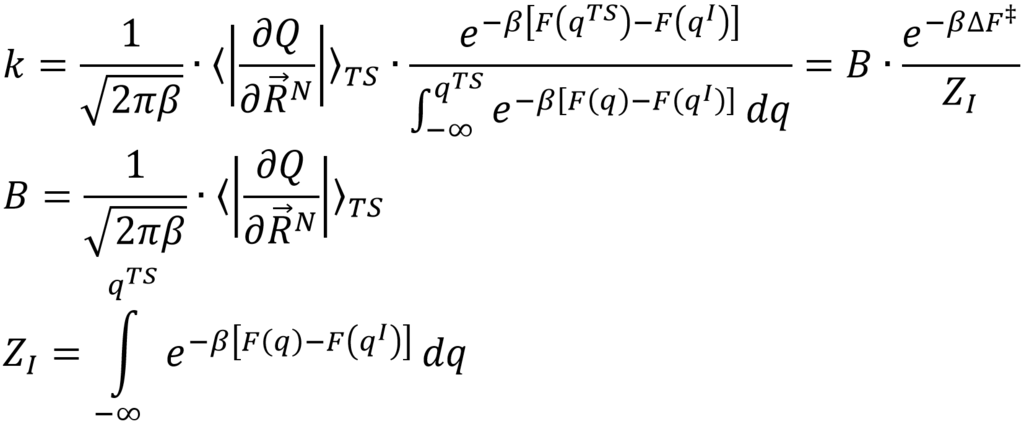
Herein, Z represents the partition function of the initial state and takes into account the entire valley in the free energy profile corresponding with the initial state, while B represents a more complex pre-exponential function. The main goal of this thesis is to investigate whether the application of this more general expression indeed leads to rates constants that are independent of the choice of the collective variable. Furthermore, some processes cannot be described by means of a single collective variable, but require 2 collective variables with a corresponding 2D free energy surface. Therefore, we will investigate how the expression can be extended towards 2D free energy surfaces. Finally, we will compare this with other methods already published in literature such as the metadynamics-inspired method of Tiwary et al. which computes the rate constant form direct molecular simulations on the fly.
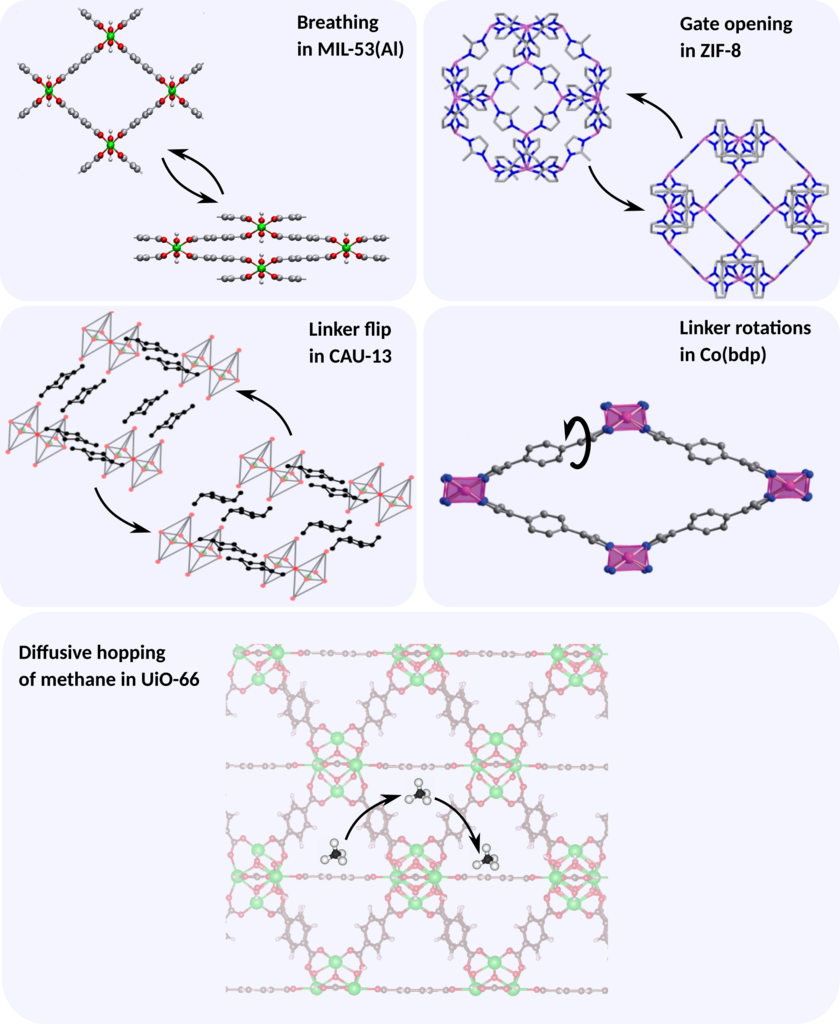
The specific processes for which the process rate will/can be investigated in this thesis are (see figure):
- Gate opening in ZIF-8: Gate-opening is a type of framework flexibility given by a crystal-to-crystal transition from a nonporous to a porous state, for example due to reorientation of the organic linkers. The results obtained in this thesis will be compared directly with experimental data available in the literature.
- Breathing in MIL-53(Al): MIL-53(Al) is a MOF that can undergo physical transformations between two (meta)stable states with a variation in its unit cell volume of up to 40%, a type of flexibility referred to as breathing. In this case, no experimental data is available, but the results will be able to give crucial insight into the frequency range for which these phase transformations occur, which will in turn be of very high value to interpret the low frequency domain of infrared spectra of this material.
- Diffusive hopping of methane in UiO-66: UiO-66 is a MOF consisting of octahedral cages that can accommodate large amounts of methane. The diffusion of methane through the framework can be modeled as a hopping process between cages for which we will compute the hopping rate and derive the diffusion constant. The results can be compared with explicit molecular dynamics simulations on a long time scale available in-house.
- Linker flip in CAU-13: Similar as for MIL-53, CAU-13 can exhibit a phase transition from a large pore to a narrow pore. However, in this case the transition is instigated by a configurational flip of the linker.
- Linker rotation in Co(bdp): Co(bdp) consists of cobalt atoms connected by means of benzenedipyrazolate linkers. The rotation of the central benzene moiety in this linker gives rise to intermediate structures which have proven crucial in the breathing behavior of this material.Engineering and physics aspects
This topic fits well within the following clusters of elective courses: Nano and Modeling. Physics aspects: development of advanced simulation techniques for estimating the transition rate of various transformations. Engineering aspects: describing the time scale in which various transformations occur in nanoporous materials.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) NANO, MODELINGKeywordsThermodynamic potential, Helmholtz free energy, Transition rate, Transition state theory, Nanoporous crystalsRecommended coursesSimulations and Modelling for the Nanoscale
