Spanning the gap from Schrödinger to Newton by deriving a classical force field from quantum mechanical training data for zeolites
Spanning the gap from Schrödinger to Newton by deriving a classical force field from quantum mechanical training data for zeolites
Promotor(en): L. Vanduyfhuys /25237 / Model and software developmentBackground and problem
Most molecular simulations that are currently applied, rely on the Born-Oppenheimer approximation. Herein, one first solves the electronic Schrödinger equation and constructs so-called Born-Oppenheimer surfaces (also called potential energy surfaces or PES) representing the potential energy as a function of the nuclear coordinates. Next, this PES is used to solve the nuclear Schrödinger equation. However, for molecular systems consisting out of heavy nuclei, one can approximate the dynamics of the nuclei by means of classical mechanics, in other words by solving Newtons equations of motion. Even though this represents a huge reduction in complexity, molecular simulations using the quantum mechanical PES are still beyond the capabilities of current supercomputers when investigating large molecular systems (> 1000 atoms) and trace their dynamic evolution over large periods of time (> 1 ns). In order to make such large length and time scales accessible, one can apply an additional approximation, which is represented by the titular force fields.
When using a force field in a molecular simulation, one does not compute the potential energy and forces corresponding to a particular point on the PES by solving the electronic Schrödinger equation. Instead, the PES is locally approximated by means of a well-chosen mathematical expression. Such expression starts from the many-body expansion of the potential energy V in a sum of two-body, three-body, four-body, … contributions. To further illustrate this, we consider one of the most simple, yet most widely used, expressions for a force field as given below:
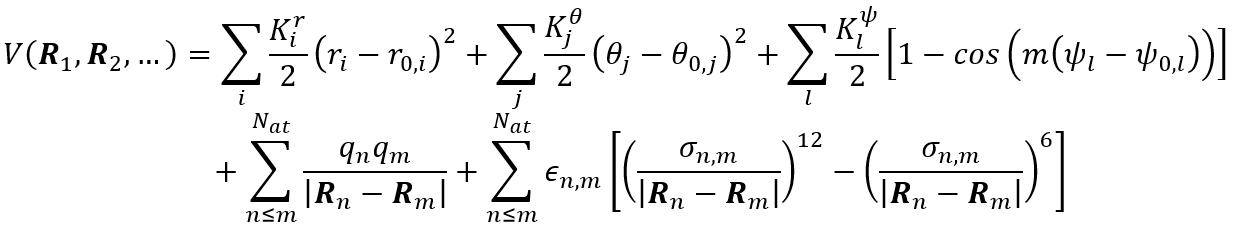
The first contribution is a 2-body term representing chemical bonds between neighboring atoms by means of harmonic springs using Hooke’s law (see figure 1). The bond lengths r figuring in this expression are dependent on the nuclear coordinates R. The second term is a 3-body contribution as function of the angle θ between two neighboring bonds (which again depends on the nuclear coordinates R). The third term is a 4-body contribution in terms of the dihedral angles. Together, the first three contributions represent to covalent energy describing the intramolecular interactions. The last two contributions cover the intermolecular interactions consisting of electrostatic interactions between fixed atomic charges (fourth term) and van der Waals interactions by means of the Lennard-Jones potential (fifth term). Al these contributions contain parameters that are a priori unknown, such as the equilibrium bond lengths r0 , the force constants Kr , … As such, the development of a new force fields boils down to choosing the appropriate mathematical form as well as estimating the best suited values for the unknown parameters.
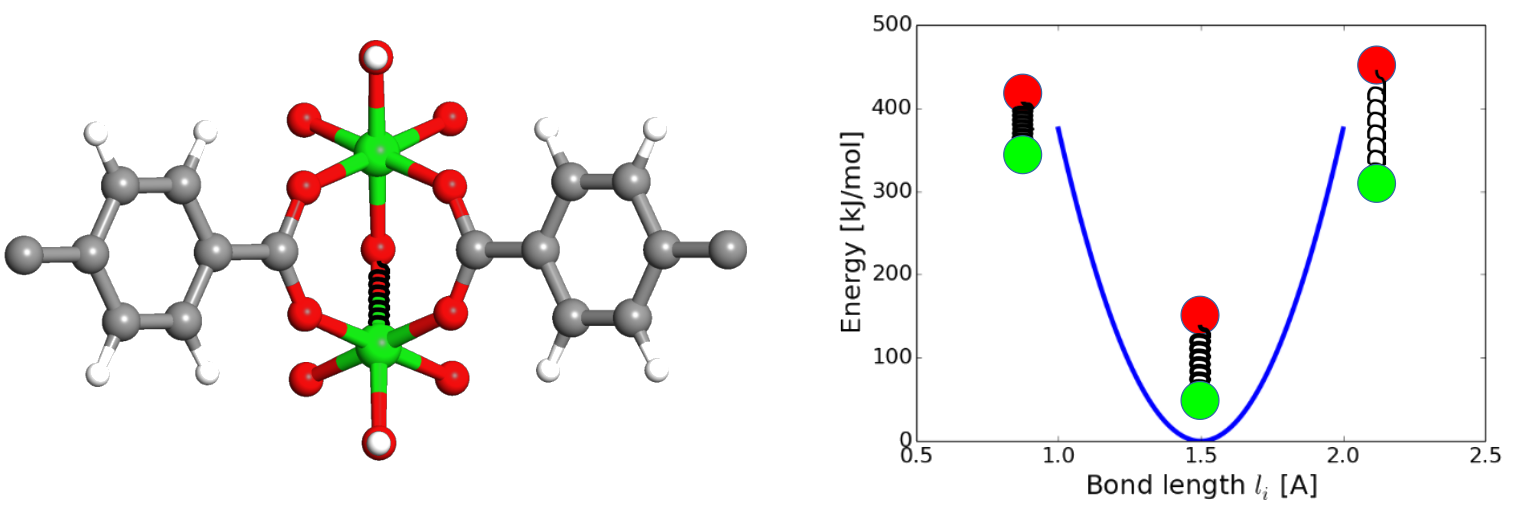
Figure 1: Illustration of the potential energy contribution of harmonic bond terms in a force field (right) associated with chemical bonds in a molecular structure (left).
Goal
At the Center for Molecular Modeling, we have developed a state-of-the-art methodology to derive new force fields [1,2,3]. This approach, which is implemented in software packages Horton [4] and QuickFF [5], estimates the unknown parameters such as covalent force constants and atomic charges in such a way that they reproduce well-chosen quantum mechanical input data as well as possible. This methodology has been well tested for various nanoporous crystalline materials such as covalent organic frameworks (COFs), which are purely organic, and metal organic frameworks (MOFs), which are hybrid organic-inorganic. However, it has not yet been applied to construct force fields for the purely inorganic nanoporous materials known as zeolites. Zeolites, depicted in the figure below, are nanoporous (i.e. have empty voids on the nanoscale) aluminosilicate (i.e. consist of Al, Si and O) minerals (i.e. pure crystalline materials that can be found in nature), which have applications in wide array applications including cat litter, softening of water, refinement of crude oil and chemical catalysis. One of the known difficulties of developing zeolite force fields is the treatment of the electrostatic interactions as well as an accurate representation of the floppy Si-O-Si bend terms.
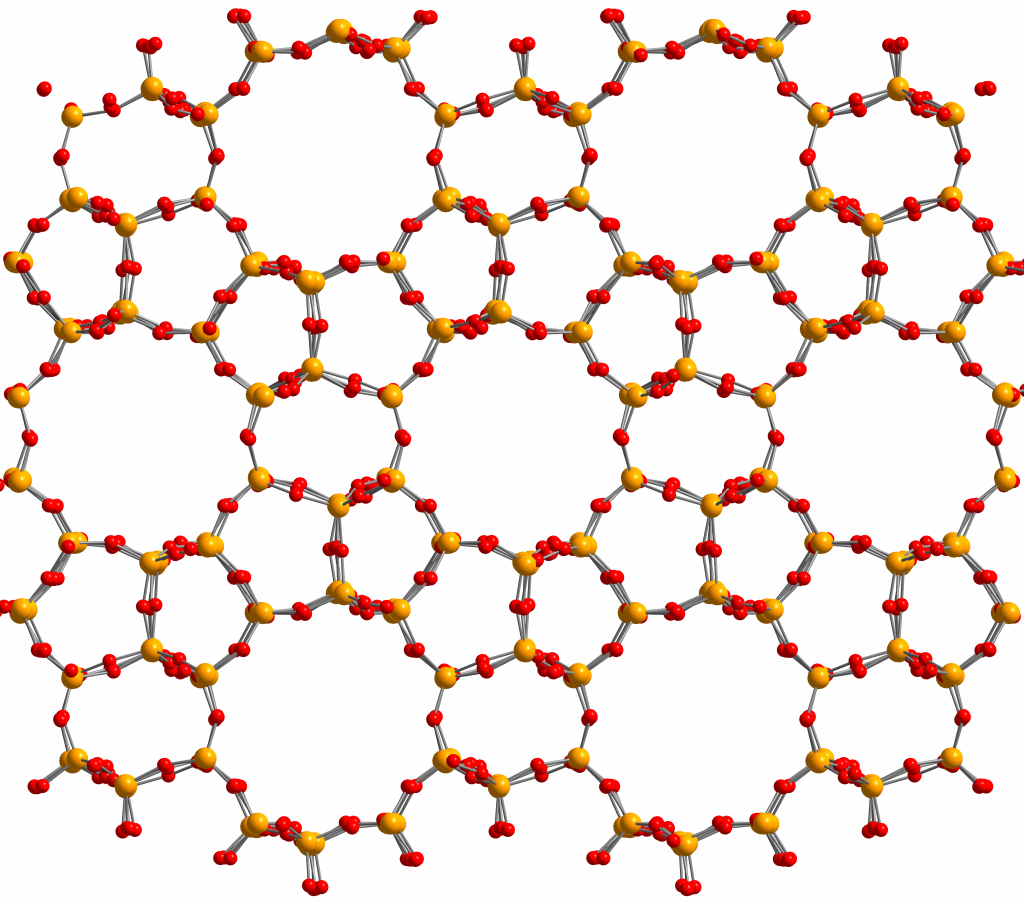
Figure 2: Illustration of the nanoporous molecular structure of the zeolite ZSM-5. Yellow balls correspond to Si, red balls to oxygen.
In this thesis, the student will derive force fields for well-characterized zeolite frameworks such as MFI, FER, AFI, BEA, CHA, … for which experimental and theoretical data are available. Furthermore, for frameworks containing relatively little atoms (e.g. CHA with 108 atoms) a comparison with periodically generated ab initio data will be performed. More specifically, the student will first make himself/herself familiar with the methodology using Horton and QuickFF. As such, (s)he will derive force fields for the previously mentioned zeolites and perform various molecular simulations that allow to compute the structural (equilibrium geometry), mechanical (bulk modulus), thermal (thermal expansion coefficient) and adsorption properties (water and methanol uptake). By comparing with experimental and/or computational data from literature, the force field will be validated and possible weaknesses can be identified. Finally, the student will be encouraged to suggest possible improvements to the force field to allow for a better validation
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]KeywordsQuantum mechanics, Born-Oppenheimer surface, potential energy, force field, electrostatic interactions, chargesReferences
[1] L. Vanduyfhuys et al., J. Comput. Chem., 2018, 39(16), 999
[2] L. Vanduyfhuys et al., J. Comput. Chem., 2015, 36(13), 1015
[3] T. Verstraelen et al., J. Chem. Theory Comput., 2016, 12(8), 3894
[4] HORTON, https://theochem.github.io/horton/2.1.1/index.html
[5] QuickFF, http://molmod.github.io/QuickFF/
