Problem statement

Computational simulations have for decades become an invaluable tool to gain a fundamental understanding of the properties of materials at the atomic scale. To study materials containing a large number of atoms, one often relies on force fields, which are composed of analytical functions describing the interatomic interactions. These force fields are preferably derived from ab-initio calculations, as no experimental input is required in this case. Recently, an intermolecular force field was published in our group which requires as input only the ab-initio electron density of the molecule(s) under study.[1] Although such ab-initio calculations are relatively cheap for small molecules, the computational cost quickly increases with increasing system size. This prevents the derivation of accurate force fields for very large molecules or periodic structures. Therefore, a computationally efficient method to obtain a partitioning of the electron density into atomic fragments of large systems is a very relevant avenue for research. We propose the use of neural networks for the prediction of the partitioned density, solely from the input of the geometry of the molecule (see Figure 1).

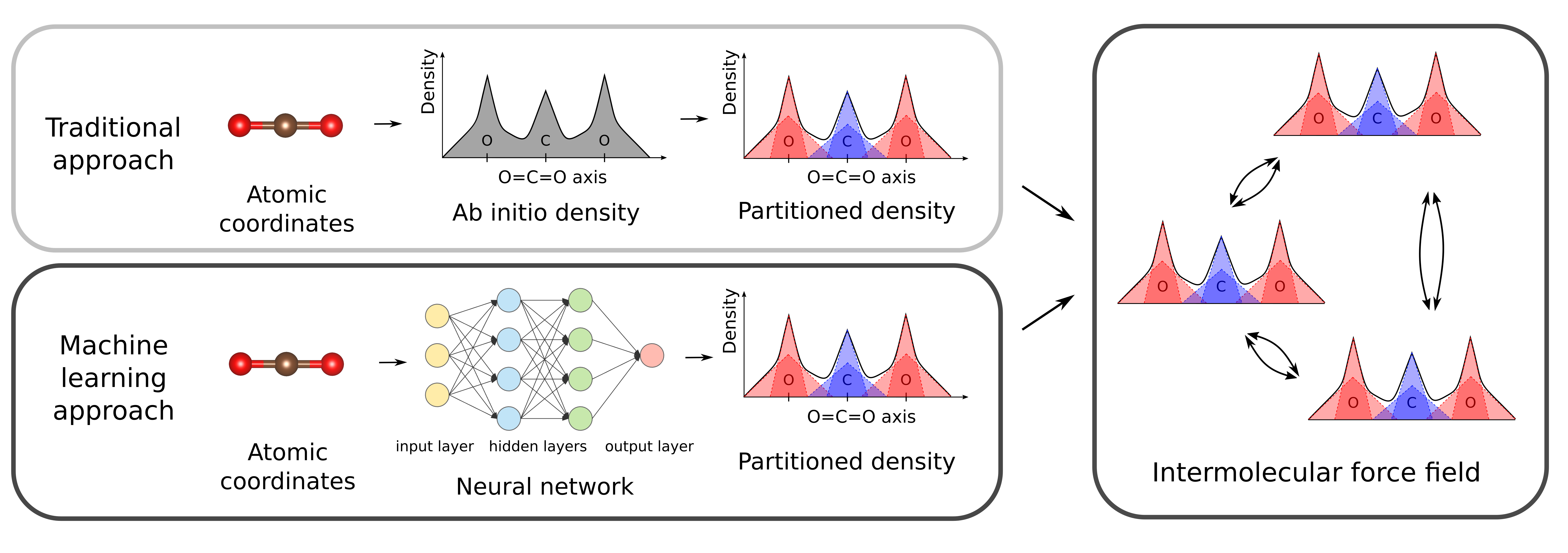
Figure 1. Traditional and machine learning approach to derive an atomic density partitioning for intermolecular force fields.

Objectives

The first step in this thesis is a critical evaluation of an existing kernel-based approach from the literature.[2] Its performance on a challenging set of zwitterionic structures will be assessed. The model is limited to neutral molecules containing only C, N, H and O atoms, and can not be used to construct force fields for ionic molecules and liquids.

The second objective is therefore to construct a neural network model, based on an existing architecture called SchNet[3]. This network was originally designed to predict the energy of a molecule, and it will therefore be modified to yield the partitioned densities of the molecule. To train the model, the ab-initio density of molecules in the existing QM9 dataset[4], as well as ionic molecules from several datasets will be calculated. The prediction error on the total and partitioned densities will be evaluated, and if not satisfactory, further modifications will be made to the network.

In a second step, the predicted densities will be benchmarked further by calculating the electrostatic interaction between dimers from a dataset of nucleobase pairs. This will serve as a validation of the model in yielding accurate electrostatic force fields without the need for expensive ab-initio calculations.

Lastly, a complete non-covalent force field will be derived and tested on a set containing dissociation curves of ionic hydrogen bonds. In this way, the used methodology can be shown to yield state of the art force fields, requiring both no experimental input and no computationally demanding ab-initio calculations.