Molecular dynamics is used in many scientific domains to simulate a system of interest at the atomic scale, e.g. "how does a drug molecule interact with an enzyme?" or "how is a gas adsorbed in a nanoporous material?" In these simulations, interatomic forces need to be computed very efficiently, e.g. for systems counting 10⁴ to 10⁷ atoms for 10⁹ to 10¹² time steps. In principle, one should solve the Schrödinger equation for the many-body electronic wavefunction in such a system, and then derive the forces acting on the nuclei, to perform a single molecular dynamics step. However, even approximate electronic structure theories are computationally far too demanding for the relevant time and length scales. Instead, force-field models are used, in which interatomic forces are modeled directly as a function of internuclear distances, without even trying to approximate the electronic wavefunction.

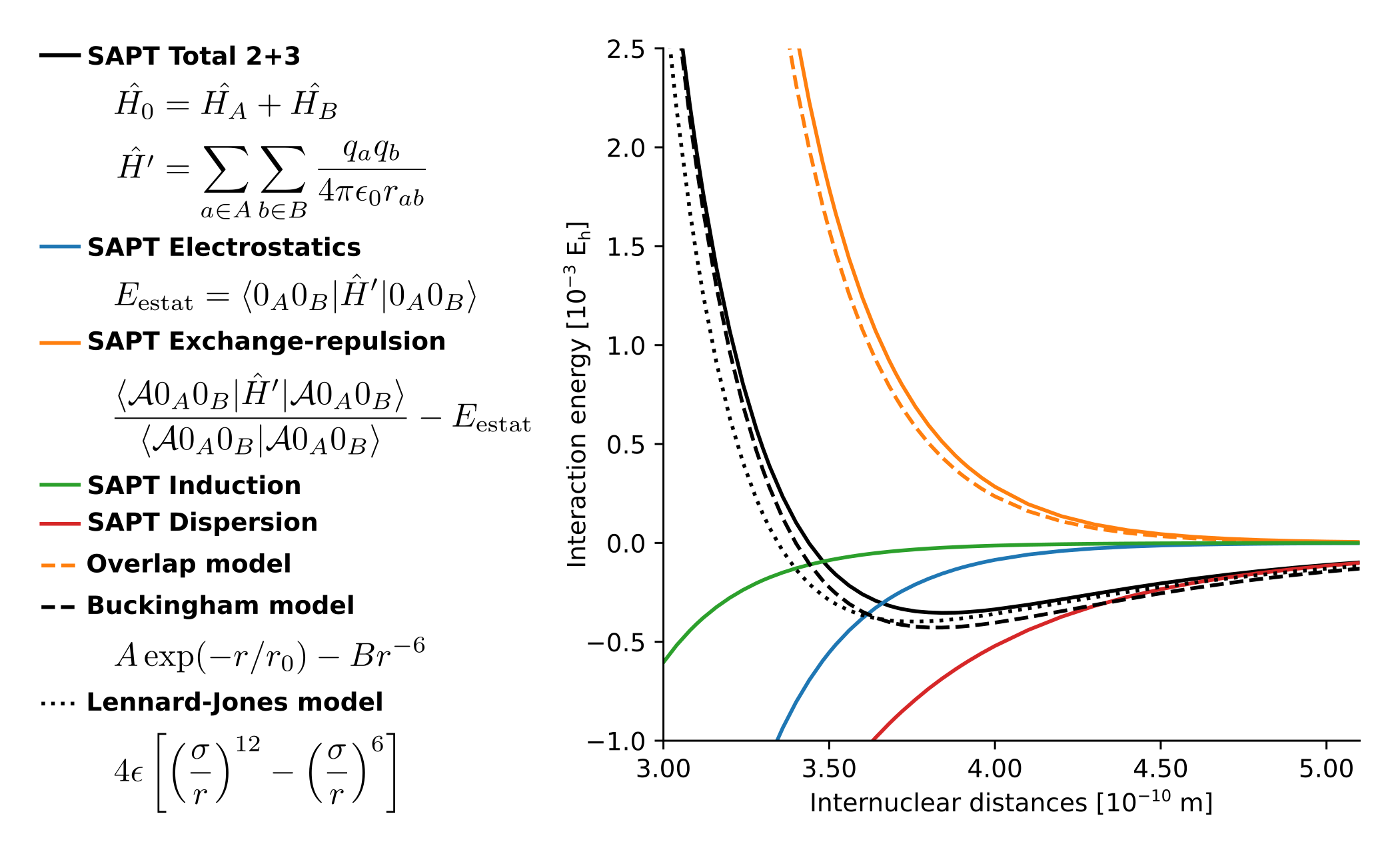
Figure 1. comparison of SAPT with some force field models for the argon dimer.

The simplest force field is the Lennard-Jones model, see Fig. 1, which is suitable for noble gases. More complex systems exhibit different types of interatomic forces, for which the functional form is not as trivial. Many such models were proposed on empirical grounds, featuring a large number of fitting parameters, with little or no relation to the quantum-mechanical description of the electronic structure. This traditional approach is limited because one must estimate more empirical parameters for every new molecule or material of interest, which is a tedious and ambiguous task. Instead, it would be much more effective to derive force-field models directly from an electronic structure theory, using physically sound approximations.

We recently published a significant step in this direction, by proposing a force field for intermolecular interactions with only three adjustable parameters, the Monomer Electron Density Force Field (MEDFF). [1] The energy terms in MEDFF have a one-to-one correspondence with symmetry-adapted perturbation theory (SAPT) [2]. One of the zeroth-order terms in MEDFF is the so-called overlap model for short-range repulsion (due to Pauli exclusion) between two molecular fragments as follows:

Where ρ_a and ρ_b are the electron densities of the isolated fragments. While this is a well-known model, there is no formal derivation, which could reveal the (system dependent) prefactor or which could lead to refinements of the overlap model.

The overall goal of this thesis is to derive mathematical expressions for force-field models directly from SAPT, and to validate these models with computational assessments. In MEDFF, the overlap model is a leading term that still contains some empirical ingredients, which will be addressed first. (Higher-order terms are considered optionally.) A preliminary formal derivation of the overlap model will be made available, which can be used as a starting point for this thesis. The computational assessments will be carried out on the so-called S66x8 dataset. This is a database of intermolecular interaction between small molecules, for which high-level electronic structure calculations are still feasible and available as a benchmark for more approximate models. Also electronic densities and related properties of the molecules in the S66x8 dataset can be trivially computed on suitable numerical integration grids.

[1] S. Vandenbrande, M. Waroquier, V. Van Speybroeck & T. Verstraelen (2017) The Monomer Electron Density Force Field (MEDFF): A Physically Inspired Model for Noncovalent Interactions. Journal of Chemical Theory and Computation, 13(1), 161–179. https://doi.org/10.1021/acs.jctc.6b00969

[2] Stone, A. J. The Theory of Intermolecular Forces, Second edition.; Oxford University Press: Oxford, 2013.