Probleemstelling:

Nanoporous materials have attracted much attention in the past decades due to their impressive potential for applications in the field of natural gas storage, detection and separation of gases, or even as effective drug delivery systems. An example of such nanoporous materials is given by the so-called metal-organic frameworks (MOFs), which are hybrid materials consisting of inorganic bricks connected to each other through organic linkers. Due to their porous nature and favorable interactions with guest species, they have been proven to exhibit extra-ordinary adsorption properties. Several modeling techniques exist to investigate these adsorption properties. On the one hand, one could consider direct molecular simulation by performing Monte Carlo in the grand canonical ensemble (GCMC). While these simulations are very accurate, they tend to be computationally expensive, which limits their applicability. On the other hand, one can express the Helmholtz free energy F in the canonical ensemble by means of a parameterized expression in the mean-field approximation.

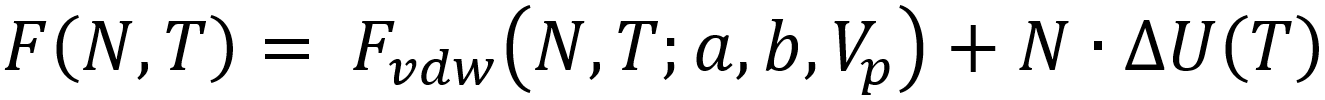
Herein, Fvdw represents the van der Waals equation of state and ΔU the mean adsorption energy. The density is approximated to be homogeneous within the pore volume Vp, and the total number of particles adsorbed N can be estimated by means of a Legendre transformation to the grand canonical ensemble:

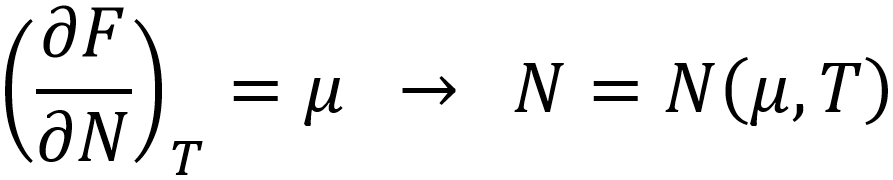
Such models have been proven capable of describing the adsorption isotherm of various complex metal organic frameworks at temperatures above the critical temperature. Unfortunately, these models are not applicable below the critical temperature, due to the approximation of a homogeneous density. Furthermore, they require input such as the van der Waals parameters a and b, as well as the pore volume Vp and mean-field adsorption energy , which are not straightforward to estimate from molecular simulation. It is in this context that classical Density Functional Theory provides a powerful alternative.

Density functional theory (DFT) was originally developed as a quantum mechanical approach to determine the electronic structure of many-body molecular systems at 0 K. In contrast to wave function based methods, which try to solve the Schrödinger equation directly, DFT describes the system in terms of the electronic density. A crucial quantity in this framework is the energy functional E[ρ], which represents the ground state energy of the system at 0 K for a given trial electronic density ρ with a fixed total of N electrons. By finding the density that minimizes this energy, one retrieves the true ground state density. Inspired by this modeling technique, physicists developed its classical analogue, i.e. classical density functional theory (cDFT), for the calculation of the density profile ρ(r) of classical particles subject to an external potential v(r) and an interaction potential w(r). It differs from its quantum mechanical big brother in three different aspects. First, the particles do not have to obey the quantum statistics of fermions, i.e. the Fermi-Dirac distribution, but the classical Maxwell-Boltzmann statistics. Second, we are interested in computing the density at finite temperature T>0 K. Third, the density is not constraint to contain a total number of N particles, instead the chemical potential μ is controlled. As a result, the density profile is obtained by minimizing the grand potential Ω, i.e. the thermodynamic potential in the μVT ensemble, which is expressed as a functional of a trial density ρ and minimized towards this density to find the true density:

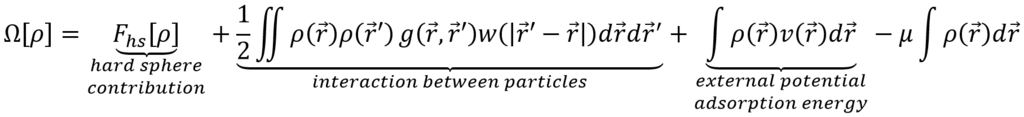
Doelstelling:

In this thesis, the student will familiarize him/herself with classical density functional theory and implement an algorithm for the solution of the cDFT equations in a Python package. In the first stage, the implementation will first be tested on two test applications: (1) a gas/liquid without an external potential at super/subcritical temperature and (2) a gas at supercritical temperature in the presence of a gravitational field. While the first test system will serve as a model for the phase transition in bulk fluid as well as for the bulk pair correlation distribution g(r,r’), the second system will serve as a simplified model for the atmosphere of Earth. In the second stage, the implementation will be applied to describe the adsorption of guest species, such as methane and carbon dioxide, in metal organic frameworks such as MOF-5. As such, we aim to investigate three subjects:

1. Compare adsorption isotherms of cDFT with the mean-field model.
2. By gradually changing the temperature and investigating the evolution of the density profile for the species adsorbed inside the pores, we will investigate the impact of subcritical temperatures on the adsorption behavior and investigate the temperature dependence of the mean adsorption energy.
3. By systematically increasing the chemical potential µ, which also increases the total number of particles N adsorbed, we will investigate the correlation between the mean adsorption energy and the number of adsorbed particles in order to evaluate the mean-field assumption.