Background and problem

As many microscopic phenomena are not directly accessible experimentally, computational modelling is often an indispensable tool to gain a more fundamental insight into these phenomena. The dynamics of complex structural transformations between different (meta)stable states of molecules or crystals are extremely difficult to monitor experimentally, as they are determined by a complex free energy surface which depends on many degrees of freedom. In this thesis topic, we focus on a particular class of nanoporous materials, so-called metal-organic frameworks (MOFs), with promising applications in gas storage, gas separation, catalysis, drug delivery… These materials are also known for their rather intriguing responses to certain triggers. A few examples of such atypical behaviour include negative linear compressibility, where upon exerting pressure, the material expands along one or more directions instead of contracting; negative thermal expansion, where the material contracts upon heating rather than expanding; and negative gas adsorption, where the MOF releases gas from its pores when the gas pressure of the surroundings is increased. These peculiar response properties are inherently linked to the unique building block concept of MOFs. Their structure, composed of metal clusters stitched together by organic linkers (Figure 1), yields a broad variety of stronger (covalent, coordinative) and weaker (dispersive, stacking, hydrogen bonding) interactions. In combination with their nanoporosity, this allows for extraordinary flexibility under external stimuli, so that MOFs can transform between various phases often accompanied by substantial volume changes while maintaining their structural integrity (Figure 1). This ability can for instance be exploited in the design of nanosensors and shock adsorbers.

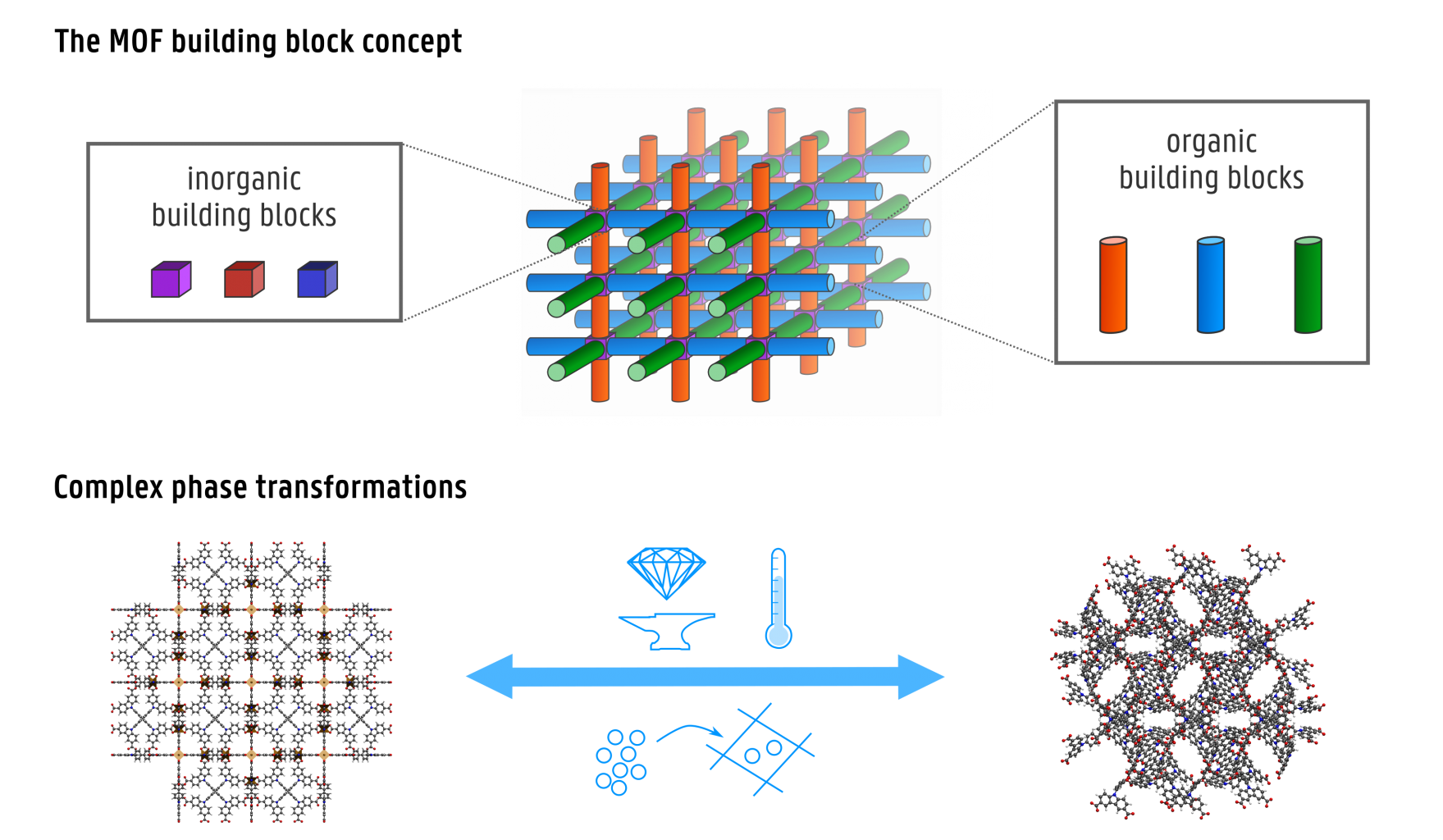
However, to fully understand and tailor the flexibility mechanisms in these materials, a thorough investigation of the underlying free energy surfaces is required.

To sample these free energy surfaces, regular sampling techniques such as molecular dynamics (MD) simulations, in which Hamilton’s equations of motion are integrated throughout time, are insufficient. Given that most phase transformations are activated processes, characterized by significant energy barriers, they only occur rarely in MD simulations. Therefore, enhanced sampling techniques are used to improve the sampling of the free energy surface in specific well-chosen directions. These directions cannot be chosen randomly, but have to drive the phase transformation and are then called collective variables. This set of variables should be as small as possible to reduce the required computational effort, but should also be sufficiently large to cover all the essential information of the transition.

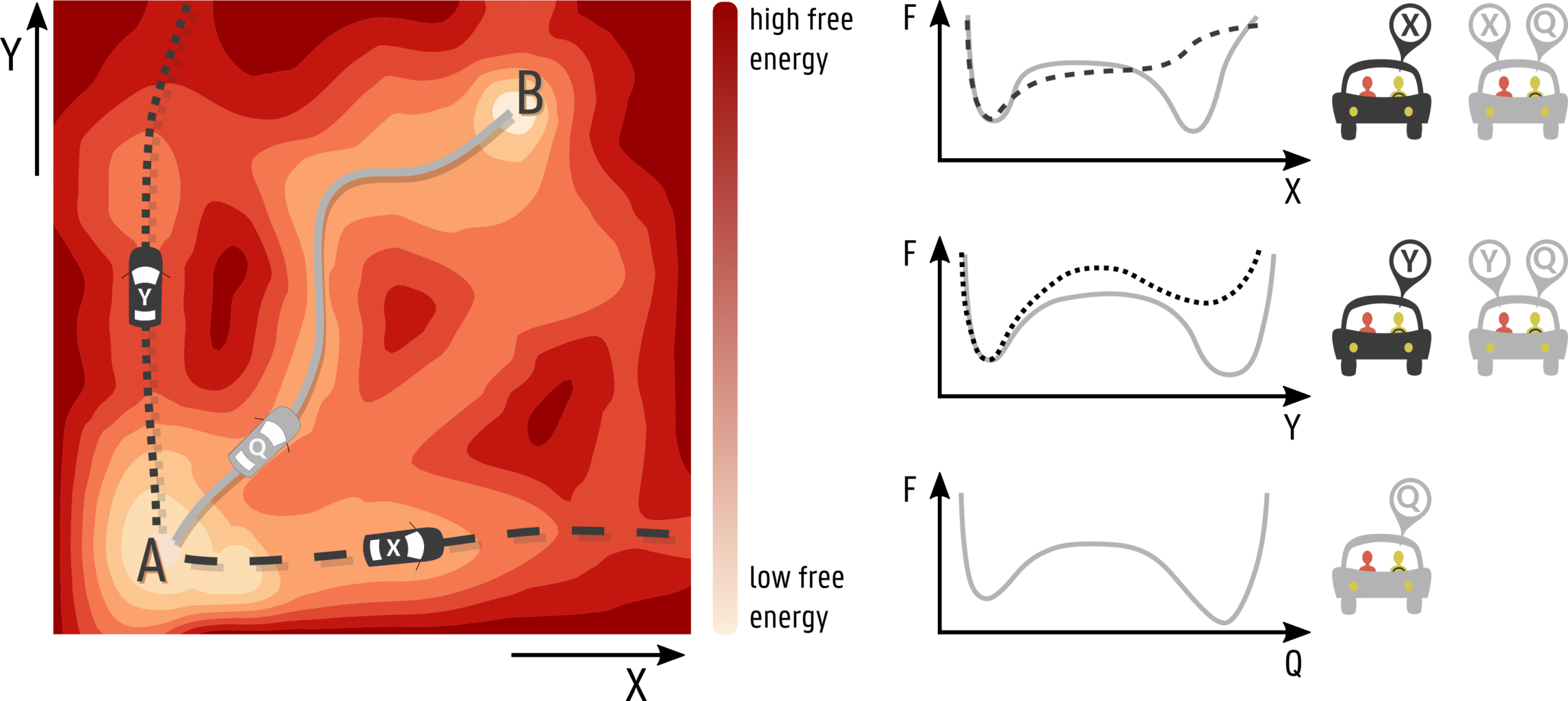
The importance of choosing suitable collective variables is highlighted by the figure below. In this figure, a hypothetical (and unknown) free energy surface is represented for which we want to sample the A—B transition. If one would start from the stable minimum A and bias the sampling only along the X-direction, the final state B would never be reached, even though X can discriminate between the initial and final states. This results in an incorrect one-dimensional free energy profile as a function of X. The same holds for a bias along the Y-direction. To reach the minimum B, one has to construct a collective variable Q that is able to drive the transition in order to obtain the correct free energy profile. For complex high-dimensional free energy surfaces, this is however a non-trivial task. Currently, the selection of collective variables is mainly based on physical insight and on experimental observations as there are no clear selection rules to obtain a small yet adequate set of collective variables. This thesis aims to tackle this problem by a systematic application of machine learning techniques to identify an essential set of variables for various MOFs with different types of flexibility.

Goal

In a first step, the thesis student will obtain insight in the problem by applying dimensionality reduction machine learning techniques on a reference MOF with a topological flexibility: CoBDP [1]. The flexibility of this material can be effectively described by using the unit cell volume as a collective variable, making this a suitable benchmark material for newly proposed machine learning methods. The input required by the machine learning algorithms comprises a set of configurations that cover the relevant transitions, which can be obtained for instance from MD simulations at increased temperatures (to facilitate the transitions). A first interesting machine learning technique to be tested is the linear time-lagged independent component analysis (TICA) [2], which is an extension of the well-known principal component analysis technique. Instead of focusing on the motions with the largest amplitudes, TICA identifies the slowest motions. The most important parameters contributing to the slowest mode(s) are then used as collective variables in enhanced sampling simulations.

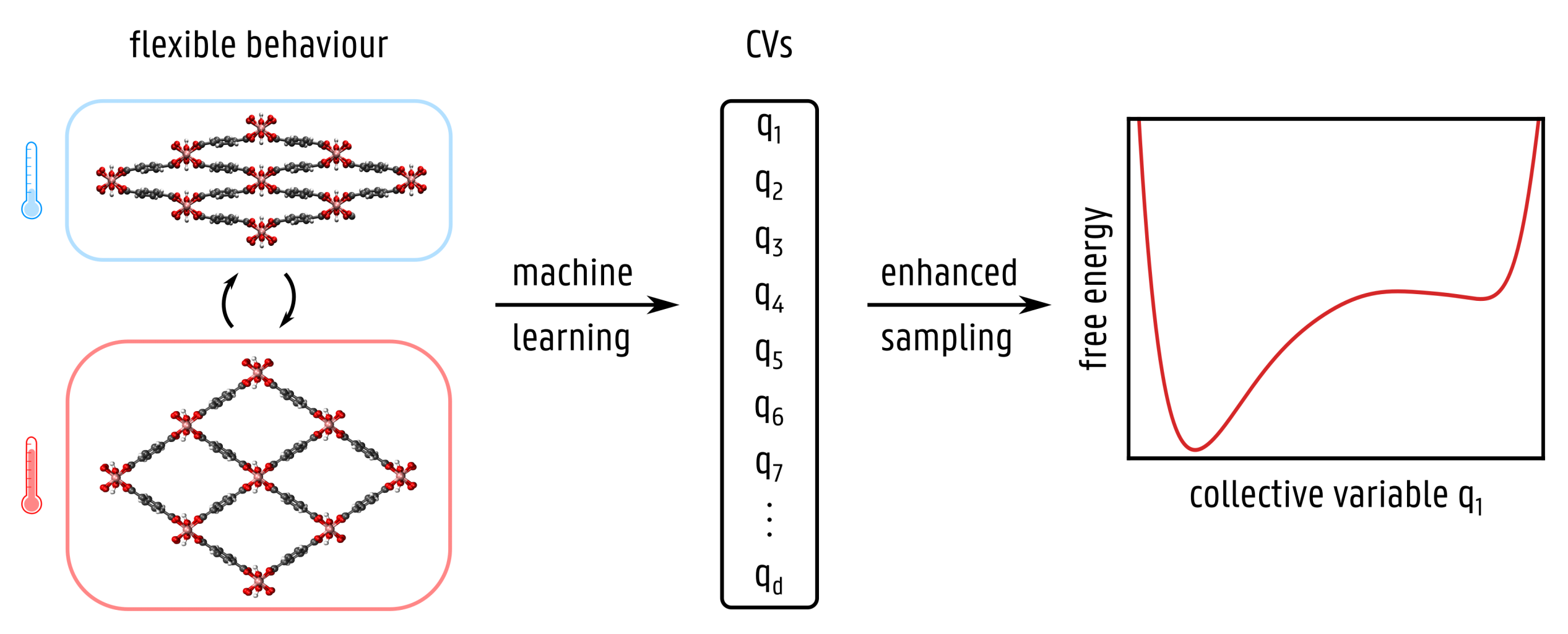
However, the main drawback of this and other linear techniques is that the user has to identify all relevant input variables (features) for the algorithm. Therefore, more recently developed non-linear techniques will also be investigated to automatically select non-linear combinations of the Cartesian input coordinates. Within the class of non-linear unsupervised machine learning techniques, we will focus on state-of-the-art methods such as time-lagged auto-encoders [3] or neural networks [4]. The goal of this thesis is to enable – in an automated fashion – the selection of suitable collective variables for materials that display different types of flexibility. In this respect, both materials with a topological flexibility, such as CoBDP and DMOF-1(Zn), as well as materials with a linker flexibility, such as DUT-49(Cu), will be investigated.

The student will be actively coached to make him/her acquainted with the advanced simulations techniques early in the thesis year and to transfer necessary programming skills needed to perform the research. Besides implementing the methodology described above, the student will also become acquainted with several new theoretical principles.