This thesis will study mass transport in inhomogeneous and anisotropic media. In simple homogeneous media such as pure liquids, the diffusion constant D is obtained from the slope of the mean square distance (MSD) versus time (t), i.e. MSD=6Dt. However in more complicated media, D is position-dependent (inhomogeneous) and might behave as a tensor (anisotropic), for which advanced methodologies need to be developed.

Lipid membranes, omnipresent in the human body, are examples of such highly inhomogeneous and anisotropic systems that are studied at the Center for Molecular Modeling. Biological membranes consist of phospholipid bilayers, with hydrophobic tails pointing inwards and a hydrophilic head pointing towards the water phase (Fig. 1). Oxygen, water, other small permeants, or medicinal molecules all need to diffuse through such membranes to reach the organelles. The diffusion depends on the position/orientation in the membrane. For instance, diffusion is expected to be slower in the dense head group region than in the tail region.

Lately, ordered domains have been detected in membranes, called rafts (Fig. 1). These rafts are rich in cholesterol and contain sphingomyelin, a specific group of phospholipids. These ordered domains are surrounded by disordered domains that are poor in cholesterol. It has been suggested that rafts play a role in signal transduction and intracellular transport through their interaction with proteins embedded in the membrane. Indeed, the existence of two phases – ordered versus disordered – adds more inhomogeneity to the membrane, and must have consequences for the transport of molecules through the membranes.

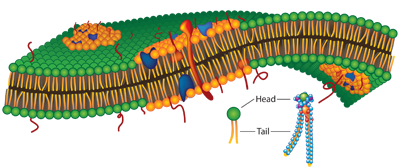
Fig. 1. A bilayer of lipid molecules (green heads, yellowish tails) is studded with proteins (various shapes and colors). The orange sections represent lipid rafts, which are areas of higher lipid density that attract and concentrate certain proteins, suggesting that the cell membrane might play an active role in regulating protein function. The inset shows a phospholipid. Oxygen mobility is suspected to be different in the rafts.

This thesis focuses on the transport of molecular oxygen, which is of utmost importance for the energy household of the cell. It is suspected that oxygen diffusion is different in the ordered than in the disordered domains. Since oxygen diffusion is difficult to measure experimentally, explicit molecular dynamics simulations are a valuable tool to get information at the atomistic scale.

Goal

The primary goal of this thesis is to study the diffusive pathways followed by oxygen molecules through the membranes and to characterize the inhomogeneity and anisotropy in ordered and disordered domains.

The first part of the thesis is the theoretical development of a theory for diffusion in a anisotropic and inhomogeneous medium. The starting equation is the Smoluchowsky equation, a generalized formulation of diffusion with a position-dependent diffusion profile, and also known as the Fokker-Planck equation. The solution of the equation is the propagator, which plays the role of a Green’s function: it gives the probability that particles have diffused over a certain distance in a given lag time. Diffusion in a homogeneous and isotropic medium is described by a simple Gaussian function, but in anisotropic and inhomogeneous media the solution of the Smoluchowsky equation is seldom available analytically. Therefore the propagator will be determined from the simulated trajectories with inverse Monte Carlo. Experience with this technique is already present in the Center for Molecular Modeling for membranes without rafts. For a system with rafts, a new theoretical extension will need to be developed.

The second part of the thesis is the practical implementation and thorough validation of the new theory. A system with and without rafts will be considered, with a mixture of ordered and disordered domains. Diffusive oxygen trajectories will be simulated with the CHARMM software package. The post-processing of the molecular dynamics trajectories will provide us with detailed information on the oxygen pathways through the cell membranes. The new theory for anisotropic ordered/disordered domains should give information on how diffusion occurs within and outside the rafts.

The research question of anisotropic diffusion is here described for oxygen mobility, but the concepts are applicable in other anisotropic media as well, such as diffusion through porous crystals, which are also studied at the Center for Molecular Modeling. The topic combines biophysics, statistical physics, method development, implementation, computer experiments, statistics, and physical insight in the biomedical research field.

Mobility: This research topic will be conducted in the framework of a strong international network. If possible the student will be actively involved in work discussions with collaborative partners (National Institutes of Health, Washington DC, USA and Max Planck Institute of Biophysics, Frankfurt, Germany). A work visit or internship can be considered (limited funding available).

Motivation Appl. Phys.: The physics aspect is the theoretical development of a diffusion propagator in anisotropic and inhomogeneous media. The engineering aspect is the development of an inverse Monte Carlo technique to extract the diffusive information from simulated trajectories.