Constructing a new localization scheme to improve the electrostatic potential of explicit electron force fields
Constructing a new localization scheme to improve the electrostatic potential of explicit electron force fields
Promotor(en): T. Verstraelen /20MODEV02 / Model and software developmentProbleemstelling:
Many properties of matter can be simulated and understood at the nanoscale, by directly solving the electronic wavefunction in the field of the nuclei. An exact solution of the electronic problem from first principles has an exponential-scaling computational cost and is only feasible for systems counting up to 40 electrons. However, in many disciplines that employ molecular simulations, one is interested in macromolecular systems counting 105 or more electrons, e.g. when simulating an entire protein or a cell membrane. (See Fig. 1.) In such scenarios, one typically uses force-field models, in which electrons are not treated explicitly. Only effective interatomic interactions are computed, and due to a lack of physically sound approximations, one usually employs very empirical models.
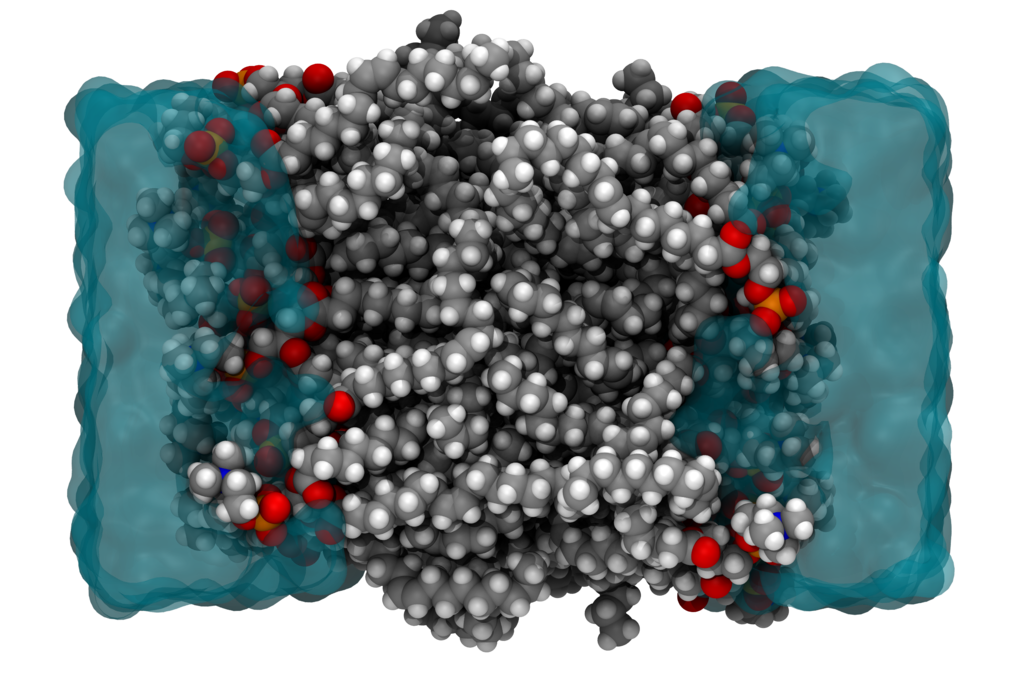
Figure 1. The cross section of a cell membrane from a molecular dynamics simulation.
In conventional force fields, the only explicit particles are "atoms". Each atom represents a nucleus and a fractional number of electrons bound to it. All other electronic degrees of freedom, i.e. the large majority, are thus discarded. A new type of explicit electron force fields (EEFFs) were recently developed in our group, which describe the electronic structure in more detail, through the average positions of each electron (pair) as depicted in Fig. 2. These averages are based on the Foster-Boys maximally localized orbitals [1], one of many possible localization schemes. Any localization scheme defines a specific unitary transformation of the Kohn-Sham orbitals in DFT, which incurs no loss of information and all observables are still accessible. For example, the molecular dipole moment can be computed from the positions and charges of the nuclei and the localized electron centers.
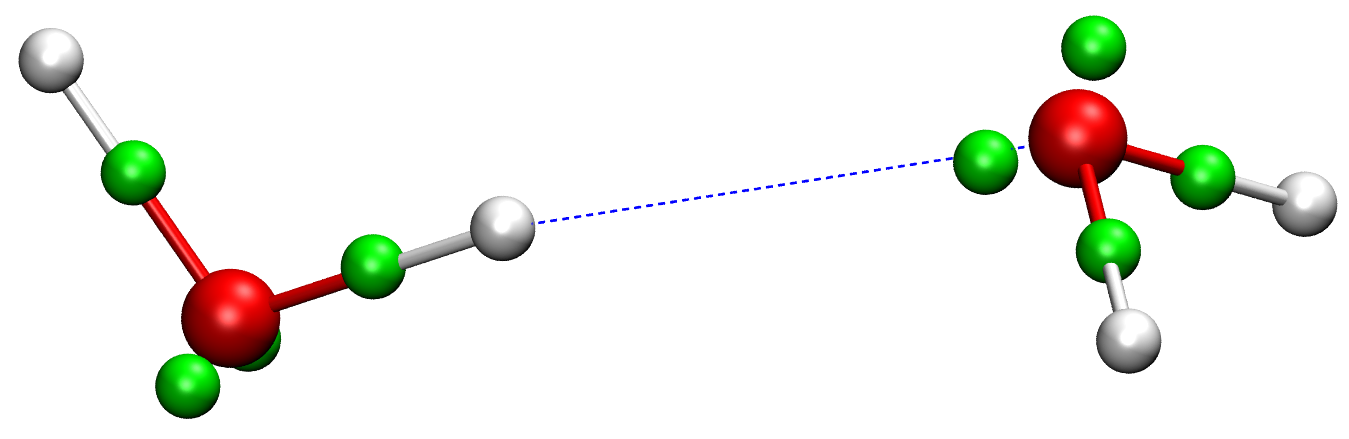
Figure 2. Electron pair Foster-Boys centers (green spheres) in a water dimer (oxygen=red, hydrogen=white).
Since the EEFFs are constructed with the average positions of the localized orbitals, all the properties of the molecular system depend on the exact location of their centers. For instance, it was observed that the molecular electrostatic potential, derived from the Foster-Boys centers and the nuclei is still a crude approximation of the true first principles potential. Furthermore, the diagonal components of the quadrupole tensor of CO2 have the wrong sign. Moreover, any EEFF will inherit the same shortcomings as its localization scheme such that improving the localization scheme is a necessity for the development of better EEFFs.
Doelstelling:
In this project, an in-depth comparison of several state-of-the-art localization schemes (Foster-Boys, Edmiston-Ruedenberg, Pipek-Mezey …) will be performed, focusing on the optimal reproduction of electrostatic properties calculated with their electron centers. The gained experience from making these benchmarks will aid the creation of a new localization scheme to enhance the electrostatics. Therefore, a cost function will be carefully constructed to optimize the unitary transformation of the Kohn-Sham orbitals. Next, it will be implemented using a unitary optimization method [2] and automatic differentiation (JAX, Tensorflow, PyTorch …). Afterwards, these insights can be applied in practice to build a new EEFF based on this localization scheme which can be trained using a machine learning force field (e.g. SchNet [3]).
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]KeywordsComputational physics, electronic structure theory, electrostatics, machine learningReferences
[1] J. M. Foster et al. Rev. Mod. Phys. 32, 300-302 (1960) https://doi.org/10.1103/RevModPhys.32.300
[2] S. Lehtola et al. J. Chem. Theory Comput. 9, 5365-5372 (2013) https://doi.org/10.1021/ct400793q
[3] K. T. Schütt et al. J. Chem. Phys. 148, 241722 (2018) https://doi.org/10.1063/1.5019779
