Metals are crucial for many constructional applications. However, metals also interact with their environment which often has undesired side-effects, such as corrosion. This limits the lifetime of a material. An important element to interact with metals, e.g. steel (Fe), the most frequently used construction material, is hydrogen. Hydrogen can cause unpredictable cracking and failure in materials (Figure 1). The issues with hydrogen flaking in the nuclear power plants of Doel and Tihange are a very well-known example of the huge consequences hydrogen can have. Moreover, the current evolution towards the hydrogen economy makes the topic extremely societal relevant.

Ample experimental research which has been performed at Ghent University demonstrates the negative impact of hydrogen on the mechanical performance of steel. It has been clearly demonstrated that ‘diffusible’ hydrogen plays a major role in this observation. Hydrogen is indeed diffusible in steel as it can travel through the metal crystal structure at room temperature at measurable rate. Experimental set-ups constructed in the group of Prof. Verbeken allow to obtain a macroscopic value for the hydrogen diffusion coefficient, but the fundamental understanding of the interaction between a single hydrogen atom and the Fe crystal structure still presents a relevant knowledge gap. Simulations might provide an important asset to help increase our understanding on the interaction between hydrogen and the steel microstructure.

In simulations, a trajectory of the particles may be followed by integrating Newton’s equations, which provides detailed insight in the diffusion mechanism at the atomic scale. For a light element like hydrogen, quantum mechanical (QM) effects come into play, where transport is aided by hydrogen tunneling (Figure 2). The motion of hydrogen needs a quantum treatment, by either solving the Schrodinger equation numerically or by using approximate quantum methods. While electron tunneling and more generally electrochemical quantum calculations are widespread, there is very limited work - nor insight – in hydrogen tunneling in solid state materials. There is thus a clear need for a framework to study hydrogen transport that builds up from basic modeling in homogeneous Fe crystals, up to the complex steel structures with grain boundaries.

Figure 1. Hydrogen crack of about 10 micrometer in steel with a brittle part, where hydrogen caused smooth brittle cracking (as if breaking a porcelein vase), and a ductile part, where the microstructure is plastically deformed (as if getting a dent in your car door).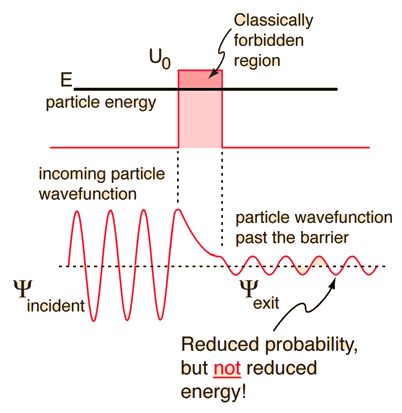

Figure 2. According to quantum mechanics, a particle can cross a barrier that is classically forbidden. The probability of this tunneling behavior is non-negligible for light particles, such as the hydrogen atom.

Goal

The primary goal of the thesis is measuring the effect of H tunneling on H diffusion by using various quantum approaches and approximations, and to connect these calculations with experimental results. In a first step, a toy model of a H trapped in a periodic potential (Fe lattice) will be studied using computational physics, in order to understand how the 1-dimensional Schrodinger equation leads to H tunneling and hopping rates. Next, a 3D description of a Fe lattice will be constructed, and the diffusive behavior of Fe will be derived by running molecular dynamics (MD) simulations in the Center for Molecular Modeling. Given the high computational cost of quantum calculations, the student will be need to design a protocol for the calculations. The protocol should be computationally feasible and should still encompass the essential physics of H diffusion.

The laboratory of prof. Verbeken has developed an experimental setup that can measure diffusion coefficients measured on commercially pure Fe. This is Fe which contains a limited amount of impurities but is only treated with reasonably (in)expensive techniques. Our permeation test-up allows to build up a hydrogen permeation transient which nicely follows Fick’s law. The MD calculations will be correlated with the measurements.

Aspects

Master of Science in Engineering Physics:
Physics aspect is fundamental insight in H tunneling, mapping out the effect on transport properties, and distilling the essential aspects relevant for H tunneling in solid state materials. Engineering aspect is the construction of a methodological simulation protocol that covers the essential aspects and is computational feasible, because the embrittlement of steels by hydrogen is a high stakes material science challenge in the steel industry.

Master of Science in Sustainable Materials Engineering:
This topic investigates the embrittlement of steels by hydrogen, which is a high stakes material science challenge in the steel industry.