Mechanical (in)stability at increased temperature: why does a material break down?
Mechanical (in)stability at increased temperature: why does a material break down?
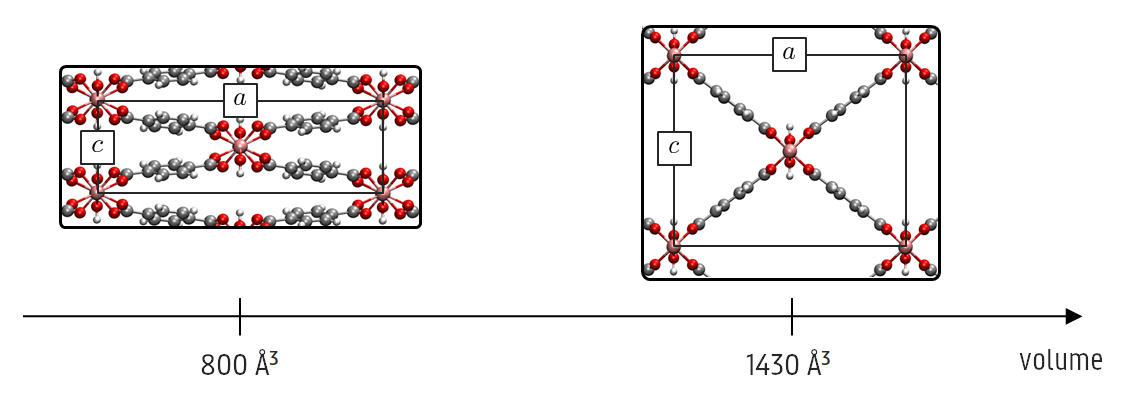
Promotor(en): V. Van Speybroeck /17NANO15 / Nanoporous materialsMetal-organic frameworks (MOFs) are crystalline materials that consist of metal oxide clusters connected by organic linkers. This results in 1D, 2D or 3D repeated structures with large cavities, i.e. periodic porous structures. The pores allow confining chemical species for several cutting-edge applications, such as gas storage, gas separation or catalysis. Contrary to most crystalline materials, some MOFs are also very flexible. Researchers discovered the adsorption of guest molecules to cause drastic deformations of the framework. This phenomenon was called the 'breathing' of the MOF, as the structure expands (large pore) or collapses (narrow pore), leading to large variations in pore size. Moreover, it was later found that breathing can also occur without guest molecules, but because of stimuli like pressure and temperature. One MOF that displays such a behaviour is MIL-53(Al) (see figure), which is most stable in its narrow-pore form at 0 K, but this phase becomes unstable at higher temperatures in favour of a large-pore crystal.
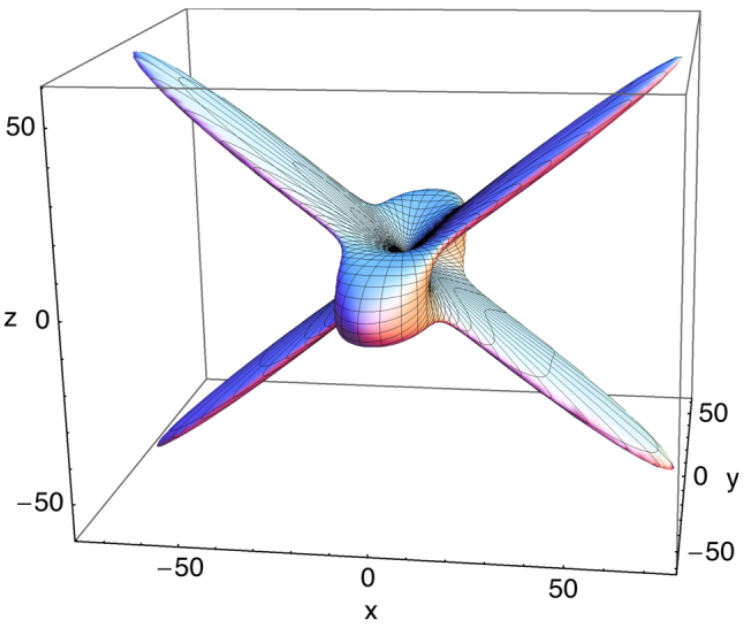
In literature, it has already been established that the breathing of metal-organic frameworks can be linked to an anisotropic stiffness of the large-pore crystal (see figure below for the anisotropic Young’s modulus of MIL-53(Al)). The material is easily deformed in one direction, but not in another. Because of this directional flexibility, the barrier between the expanding and collapsing of the pores remains small, enabling the breathing of the MOF. The mechanical stability of the material, on the other hand, can be described by the so-called Born criteria, which express the need for the elastic tensor to be positive semidefinite. As soon as one of these criteria is no longer met, the structure can spontaneously deform into another phase, such as in the case of the narrow-to-large-pore transition in MIL-53(Al). Both quantities therefore allow us to say something about the deformation behaviour of a MOF.
Goal
Despite these insights into the mechanical behaviour of flexible MOFs, it has in practice proven very difficult to determine their elastic constants. By extension, there is little knowledge on any related quantity, such as elastic anisotropy or mechanical stability. The aim of this thesis is therefore to establish temperature-dependent elastic constants from atomic-scale simulations, to better understand why materials fail at higher temperature. Two different methodologies will be compared, based on either quantum physics (density-functional theory or DFT – slow yet accurate) or classical ball-and-spring-type potentials (force fields or FF – fast yet with limited transferability). In the first case, temperature dependence will be included by means of the so-called quasiharmonic approximation, using the volume-dependent phononic and electronic density of states to build a partition function from which the free energy can be determined. In the second case, molecular dynamics (MD) will be performed to investigate the dynamic reaction of the material to temperature.
DFT has never been used before to determine the temperature-dependent anisotropic elastic constants of a complex MOF like MIL-53(Al). You will therefore first consider a model system, graphite, which contains many of the same bonding features of MIL-53(Al). Indeed, the mechanical behaviour of MIL-53(Al) is largely determined by its covalently bound, carbon-based linkers, which interact with each other through van der Waals forces. Similarly, graphite possesses a combination of strong covalent bonds between carbon atoms within a single graphene sheet and weak London dispersion interactions between the different sheets. Graphite is therefore an excellent yet challenging test system for computing accurate temperature-dependent elastic constants, either from DFT or with FF. Questions of interest are how dispersion is best described and how the anisotropic stiffness evolves with temperature. The latter quantity can be investigated using open-source tools, such as ELATE.
Based on the insights gathered from graphite, the mechanical (in)stability of MIL-53(Al) can be studied. In particular, you will need to investigate how the elastic anisotropy and Born criteria depend on temperature, eventually giving rise to the instability of the narrow-pore phase. Dispersion models may play an important role here, but anharmonicity is a well-known issue as well, which cannot be captured in the quasiharmonic approach. By comparing to MD calculations, using an in-house developed force field, you will be able to show the limitations of both the quasiharmonic approach and the used force field, and suggest possible routes for improvement. In addition to the mechanical behaviour of the material, you will be able to use the computed vibrational and electronic properties to investigate other important features of MIL-53(Al), depending on your interests. The temperature-dependent free energy difference between the two phases of MIL-53(Al), for example, expresses the energetic stability of the large and narrow pore structures. A second point of interest is the thermal conductivity of MIL-53(Al), which plays an important role in industrial applications.
Context for Engineering Physics students
Physics: use of quantum and classical mechanical models for materials modelling / Engineering: application to the mechanical properties of nanoporous materials.
- Study programmeMaster of Science in Engineering Physics [EMPHYS], Master of Science in Physics and Astronomy [CMFYST]ClustersFor Engineering Physics students, this thesis is closely related to the cluster(s) MODELLING, MATERIALS, NANOKeywordselastic constant, quasiharmonic approach, density-functional theory, Force fields, Metal-organic frameworksRecommended coursesSimulations and Modeling for the Nanoscale, Computational Materials PhysicsReferences
A. Ortiz et al., ‘Anisotropic Elastic Properties of Flexible Metal-Organic Frameworks: How Soft are Soft Porous Crystals?’, Phys. Rev. Lett. 109, 195502 (2012).
D.E.P. Vanpoucke et al., ‘Mechanical Properties from Periodic Plane Wave Quantum Mechanical Codes: The Challenge of the Flexible Nanoporous MIL-47(V) Framework’, J. Phys. Chem. C 119, 23752-23766 (2015).
L. Vanduyfhuys et al., ‘Ab Initio Parametrized Force Field for the Flexible Metal–Organic Framework MIL-53(Al)’, J. Chem. Theory Comput. 8, 3217-3231 (2012).


